题目内容
(本题满分12分)在直角坐标系xOy中,直线l的参数方程为: (t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为r=
(t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为r= cos(θ+
cos(θ+ ),求直线l被曲线C所截的弦长.
),求直线l被曲线C所截的弦长.
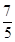
解析试题分析:将方程 (t为参数)化为普通方程得,3x+4y+1=0,………3分
(t为参数)化为普通方程得,3x+4y+1=0,………3分
将方程r= cos(θ+
cos(θ+ )化为普通方程得,x2+y2-x+y=0, ……………6分
)化为普通方程得,x2+y2-x+y=0, ……………6分
它表示圆心为(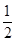 ,-
,-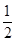 ),半径为
),半径为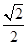 的圆, …………………………9分
的圆, …………………………9分
则圆心到直线的距离d=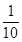 , ……………………………10分
, ……………………………10分
弦长为2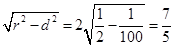 . ……………………12分
. ……………………12分
考点:直线参数方程,圆的极坐标方程及直线与圆的位置关系
点评:先将参数方程极坐标方程转化为普通方程

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
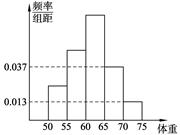
为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1∶2∶3,第1小组的频数为6,则报考飞行员的学生人数是 ( )
| A.36 | B.40 | C.48 | D.50 |
下列说法中不正确的是( )
A.对于线性回归方程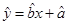 ,直线必经过点 ,直线必经过点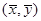 |
| B.茎叶图的优点在于它可以保存原始数据,并且可以随时记录 |
| C.将一组数据中的每一个数据都加上或减去同一常数后,方差恒不变 |
D.掷一枚均匀硬币出现正面向上的概率是 ,那么一枚硬币投掷2次一定出现正面 ,那么一枚硬币投掷2次一定出现正面 |
一个样本数据按从小到大的顺序排列为: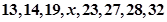 ,其中,中位数是
,其中,中位数是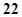 ,则
,则 等于( )
等于( )
A.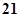 | B.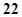 | C.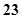 | D.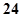 |
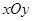 中,
中, 是过定点
是过定点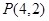 且倾斜角为
且倾斜角为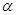 的直线;在极坐标系(以坐标原点
的直线;在极坐标系(以坐标原点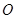 为极点,以
为极点,以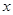 轴非负半轴为极轴,取相同单位长度)中,曲线
轴非负半轴为极轴,取相同单位长度)中,曲线 的极坐标方程为
的极坐标方程为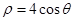 .
.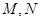 ,求
,求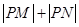 的取值范围.
的取值范围.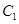 的参数方程为
的参数方程为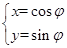 (
(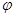 为参数),以坐标原点
为参数),以坐标原点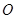 为极点,
为极点,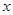 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆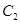 的极坐标方程为
的极坐标方程为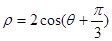 .
.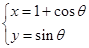 (
(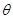 为参数),P是圆C与x轴的正半轴的交点.
为参数),P是圆C与x轴的正半轴的交点.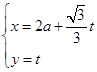 (
(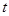 为参数,
为参数,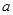 为常数且
为常数且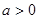 )被以原点为极点,
)被以原点为极点, 轴的正半轴为极轴,方程为
轴的正半轴为极轴,方程为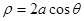 的曲线所截,求截得的弦长.
的曲线所截,求截得的弦长.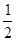 ,1),倾斜角
,1),倾斜角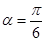 ,在极坐标系下,圆C的极坐标方程为
,在极坐标系下,圆C的极坐标方程为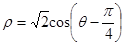 。
。