题目内容
已知圆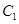 的参数方程为
的参数方程为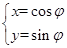 (
(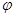 为参数),以坐标原点
为参数),以坐标原点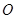 为极点,
为极点,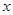 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆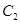 的极坐标方程为
的极坐标方程为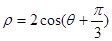 .
.
(I)将圆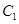 的参数方程化为普通方程,将圆
的参数方程化为普通方程,将圆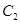 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(II)圆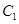 、
、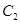 是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
(1) (2)相交,︱AB︱=√3
(2)相交,︱AB︱=√3
解析试题分析:解:I)由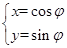 得x2+y2=1,
得x2+y2=1, 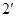
又∵ρ=2cos(θ+ )=cosθ-
)=cosθ-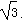 sinθ,
sinθ,
∴ρ2=ρcosθ-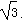 ρsinθ.
ρsinθ.
∴x2+y2-x+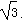 y=0,即
y=0,即

(II)圆心距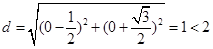 ,得两圆相交
,得两圆相交 
由 得,A(1,0),B
得,A(1,0),B ,
, 
∴︱AB︱=√3
考点:圆与圆的位置关系
点评:主要是考查了参数方程与圆圆位置关系的运用,属于基础题。

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
下列说法中,正确的是( ).
| A.数据5,4,4,3,5,2的众数是4 |
| B.一组数据的标准差是这组数据的方差的平方 |
| C.数据2,3,4,5的标准差是数据4,6,8,10的标准差的一半 |
| D.频率分布直方图中各小长方形的面积等于相应各组的频数 |
 (θ为参数),直线l经过定点P(2,3),倾斜角为
(θ为参数),直线l经过定点P(2,3),倾斜角为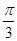 .
. (t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ.
(t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ. ,求α的值.
,求α的值.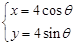 (
(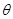 为参数),直线l经过点P(2,2),倾斜角
为参数),直线l经过点P(2,2),倾斜角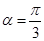 。(1)写出圆的标准方程和直线l的参数方程;
。(1)写出圆的标准方程和直线l的参数方程;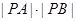 的值。
的值。 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: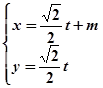 (
(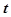 是参数).
是参数). 参数方程转化为普通方程;
参数方程转化为普通方程; ,试求实数
,试求实数 值.
值. 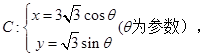 直线
直线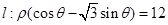
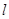 的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程;
的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程; (t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为r=
(t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为r= cos(θ+
cos(θ+ ),求直线l被曲线C所截的弦长.
),求直线l被曲线C所截的弦长.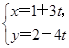 (t为参数)与直线l2:2x-4y=5相交于点B,又点A(1,2),求|AB|.
(t为参数)与直线l2:2x-4y=5相交于点B,又点A(1,2),求|AB|.