题目内容
已知圆C的参数方程为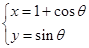 (
(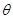 为参数),P是圆C与x轴的正半轴的交点.
为参数),P是圆C与x轴的正半轴的交点.
(1)求过点P的圆C的切线极坐标方程和圆C的极坐标方程;
(2)在圆C上求一点Q(a, b),它到直线x+y+3=0的距离最长,并求出最长距离。
(Ⅰ)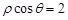 ;
; 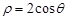 ;(Ⅱ)
;(Ⅱ) 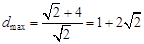 ,这时
,这时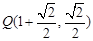
解析试题分析:(Ⅰ)求过点P的圆C的切线为: x="2," 则极坐标方程为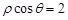 ;
;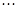 2分
2分
圆C的普通方程为: 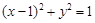 ,则极坐标方程为
,则极坐标方程为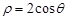
 4分
4分
(Ⅱ)设 , 5分
, 5分
则点Q(a, b)到直线x+y+3=0的距离为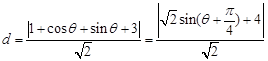
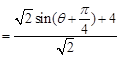 8分
8分
当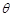
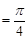 时,
时,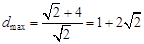 , 9分
, 9分
这时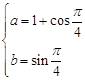 , 即
, 即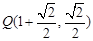 10分
10分
考点:本题考查了极坐标与直角坐标系方程的互化及点到直线的距离
点评:近几年的高考试题对选修4-4的考查都是以极坐标方程与参数方程混合命题,而且通常与直线和圆联系.这可能是前面命题涉及圆少的原因.我们在复习的过程中要注意训练化极坐标方程和参数方程为普通方程

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
我校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一、高二、高三各年级抽取的人数分别为
| A.45,75,15 | B.45,45,45 | C.30,90,15 | D.45,60,30 |
为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:
父亲身高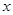 ( ( ) ) | 174 | 176 | 176 | 176 | 178 |
儿子身高 ( ( ) ) | 175 | 175 | 176 | 177 | 177 |
则
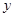 对
对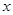 的线性回归方程为( )
的线性回归方程为( )A.
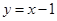 B.
B.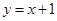 C.
C.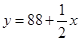 D.
D.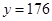
 (
(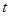 为参数),
为参数), (
( 为参数).
为参数). 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线; 的左顶点且倾斜角为
的左顶点且倾斜角为 的直线
的直线 交曲线
交曲线 于
于 两点,求
两点,求 .
. (t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ.
(t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ. ,求α的值.
,求α的值. .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: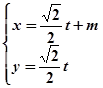 (
(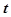 是参数).
是参数). 参数方程转化为普通方程;
参数方程转化为普通方程; ,试求实数
,试求实数 值.
值. 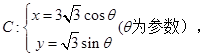 直线
直线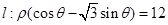
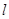 的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程;
的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程; 的参数方程为:
的参数方程为:
 (t为参数),曲线C的极坐标方程为:
(t为参数),曲线C的极坐标方程为: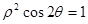 .
. (t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为r=
(t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为r= cos(θ+
cos(θ+ ),求直线l被曲线C所截的弦长.
),求直线l被曲线C所截的弦长.