题目内容
(本小题满分10分)
已知直线l经过点P(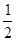 ,1),倾斜角
,1),倾斜角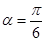 ,在极坐标系下,圆C的极坐标方程为
,在极坐标系下,圆C的极坐标方程为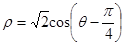 。
。
(1)写出直线l的参数方程,并把圆C的方程化为直角坐标方程;
(2)设l与圆C相交于A,B两点,求点P到A,B两点的距离之积。
(1)直线L参数方程是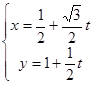
圆的普通方程是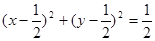
(2)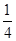
解析试题分析:(1)直线L参数方程是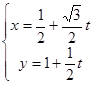
圆的普通方程是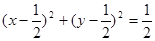 ………………………5分
………………………5分
(2)又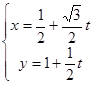 代入
代入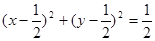 得:
得: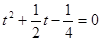
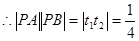 …………………………………………10分
…………………………………………10分
考点:本试题考查了直线与圆的位置关系的运用。
点评:熟练的表示直线的参数方程,以及将极坐标方程能化为普通方程,这是基本的知识点,那么在研究直线与圆的相交弦的长度的时候,可以借助于参数方程中t的几何意义,和韦达定理快速得到结论。属于基础题。

练习册系列答案
相关题目
某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本.若样本中的中年职工为5人,则样本容量为( )
| A.7 | B.15 | C.25 | D.35 |
我校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一、高二、高三各年级抽取的人数分别为
| A.45,75,15 | B.45,45,45 | C.30,90,15 | D.45,60,30 |
在2014年3月15日,某超市对某种商品的销售量及其售价进行调查分析,发现售价x元和销售量y件之间的一组数据如下表所示:
| 售价x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
由散点图可知,销售量y与售价x之间有较好的线性相关关系,其线性回归方程是:y= -3.2x+a,则a=( )
A.-24 B.35.6 C.40.5 D.40
 直线l和抛物线y2=2x相交于A、B两点,设线段AB的中点为M,求:(1)|PM|; (2)|AB|.
直线l和抛物线y2=2x相交于A、B两点,设线段AB的中点为M,求:(1)|PM|; (2)|AB|. .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: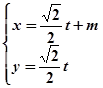 (
(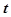 是参数).
是参数). 参数方程转化为普通方程;
参数方程转化为普通方程; ,试求实数
,试求实数 值.
值.  的参数方程为:
的参数方程为:
 (t为参数),曲线C的极坐标方程为:
(t为参数),曲线C的极坐标方程为: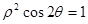 .
. (t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为r=
(t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为r= cos(θ+
cos(θ+ ),求直线l被曲线C所截的弦长.
),求直线l被曲线C所截的弦长.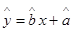 必过点( )
必过点( )