题目内容

14．已知{an}为等比数列，a4+a7=2，a5a6=-8，则a1+a10=-7．

分析 由等比数列的性质和韦达定理可得a4，a7，进而可求公比q3，代入等比数列的通项可求a1，a10，相加即可．

解答 解：由题意和等比数列的性质可得a4a7=a5a6=-8，
∴a4和a7为方程x2-2x-8=0的两实根，
解得方程可得$\left\{\begin{array}{l}{{a}_{4}=-2}\\{{a}_{7}=4}\end{array}\right.$或$\left\{\begin{array}{l}{{a}_{4}=4}\\{{a}_{7}=-2}\end{array}\right.$
当$\left\{\begin{array}{l}{{a}_{4}=-2}\\{{a}_{7}=4}\end{array}\right.$时，公比满足q3=$\frac{{a}_{7}}{{a}_{4}}$=-2，
此时a1=1，a10=-8，∴a1+a10=-7；
当$\left\{\begin{array}{l}{{a}_{4}=4}\\{{a}_{7}=-2}\end{array}\right.$时，公比满足q3=$\frac{{a}_{7}}{{a}_{4}}$=-$\frac{1}{2}$，
此时a1=-8，a10=1，∴a1+a10=-7；
故答案为：-7．

点评 本题考查等比数列的性质及通项公式，属基础题．

练习册系列答案
相关题目
3．边长为2的正方形ABCD，对角线的交点为E，则$（\overrightarrow{AB}+\overrightarrow{AD}）•\overrightarrow{AE}$=4．
4．直角坐标系中曲线C的参数方程为$\left\{\begin{array}{l}x=4cosθ\\ y=2sinθ\end{array}$（θ为参数）．
（1）求曲线C的直角坐标方程；
（2）经过点M（2，1）作直线l交曲线C于A，B两点，若M恰好为线段AB的三等分点，求直线l的斜率．
2．已知a∈R，函数f（x）=lnx-a（x-1），e为自然对数的底数．
（1）若a=$\frac{1}{e-1}$，求函数y=|f（x）|取得极值时所对应的x的值；
（2）若不等式f（x）≤-$\frac{a{x}^{2}}{{e}^{2}}$+$\frac{（1+2a-ea）x}{e}$恒成立，求a的取值范围．
9．已知某几何体的三视图如图所示，则该几何体的体积为（　　）
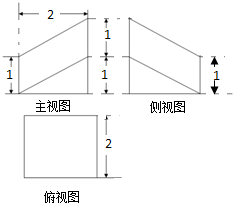
A．$\frac{14}{3}$B．4C．$\frac{10}{3}$D．3
19．从某班的科技创新比赛结果中任抽取9名学生的成绩，其分布如茎叶图所示：
（1）求这9名学生的成绩的样本平均数$\overline{x}$和样本方差s2（结果取整数）；
（2）从该9个学生的成绩高于70的成绩中，任抽取2名学生成绩，求这2名学生的成绩分别分布于[70，80），[90，100）的概率．
6．已知函数f（x）=e-x（x2+ax）在点（0，f（0））处的切线斜率为2．
（Ⅰ）求实数a的值；
（Ⅱ）设g（x）=-x（x-t-$\frac{3}{e}$）（t∈R），若g（x）≥f（x）对x∈[0，1]恒成立，求t的取值范围；
（Ⅲ）已知数列{an}满足a1=1，an+1=（1+$\frac{1}{n}$）an，
求证：当n≥2，n∈N时 f（$\frac{{a}_{1}}{n}$）+f（$\frac{{a}_{2}}{n}$）+L+f（$\frac{{a}_{n-1}}{n}$）＜n•（$\frac{1}{6}+\frac{3}{2e}$）（e为自然对数的底数，e≈2.71828）．
3．在平面直角坐标系中有一点列P1（a1，b1），P2（a2，b2），…，Pn（an，bn），…对?n∈N+，点Pn在函数y=ax（0＜a＜1）的图象上，又点An（n，0），Pn（an，bn），An+1（n+1，0）构成等腰三角形，且|PnAn|=|PnAn+1|若对?n∈N+，以bn，bn+1，bn+2为边长能构成一个三角形，则a的取值范围是$\frac{\sqrt{5}-1}{2}$＜a＜1．
11．已知函数f（x）=ax-1+lnx，其中a为常数．
（1）当a∈（-∞，-$\frac{1}{e}$）时，若f（x）在区间（0，e）上的最大值为-4，求a的值；
（2）当a=-$\frac{1}{e}$时，若函数g（x）=|f（x）|-$\frac{lnx}{x}$-$\frac{b}{2}$存在零点，求实数b的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网