题目内容
20.抛物线y2=2px(p>0)的弦PQ的中点为(x0,y0)(y0≠0),则弦PQ的斜率是( )| A. | $\frac{p}{{y}_{0}}$ | B. | -$\frac{p}{{y}_{0}}$ | C. | px0 | D. | -px0 |
分析 利用“点差法”、中点坐标公式、斜率的计算公式即可得出.
解答 解:设弦的端点的坐标P(x1,y1),Q(x2,y2),弦PQ的中点P(x0,y0),
∴2x0=x1+x2,2y0=y1+y2,
∵y12=2px1,y22=2px2,
作差整理可得2y0(y1-y2)=2p(x1-x2),
∴弦PQ的斜率是$\frac{p}{{y}_{0}}$,
故选:A.
点评 熟练掌握“点差法”、中点坐标公式、斜率的计算公式是解题的关键.

练习册系列答案
相关题目
15.函数y=cos(ωx+$\frac{π}{2}$)在[0,$\frac{π}{4}$]上为增函数,则ω的取值范围为( )
| A. | [-2,0) | B. | [-3,0) | C. | [-2,2] | D. | (0,2] |
5.已知函数f(x)=x+$\frac{a}{x}$+1的值域为(-∞,-1]∪[3,+∞),则a2008=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
12.设函数f(x)=x2-1,那么f[f(x)]=( )
| A. | x4-1 | B. | x4+2x2 | C. | x4+1 | D. | x4-2x2 |
9.“a=2”是“复数z=$\frac{a+2i}{1-i}$的对应点落在复平面的虚轴上”的 ( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
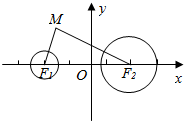 如图所示,已知定圆F1:x2+y2+10x+24=0,定圆F2:(x-5)2+y2=16,动圆M与定圆F1,F2都外切,求动圆圆心M的轨迹方程.
如图所示,已知定圆F1:x2+y2+10x+24=0,定圆F2:(x-5)2+y2=16,动圆M与定圆F1,F2都外切,求动圆圆心M的轨迹方程.