题目内容
【题目】设抛物线![]() 的准线与
的准线与![]() 轴交于
轴交于![]() ,抛物线的焦点
,抛物线的焦点![]() ,以
,以![]() 为焦点,离心率
为焦点,离心率![]() 的椭圆与抛物线的一个交点为
的椭圆与抛物线的一个交点为![]() ;自
;自![]() 引直线交抛物线于
引直线交抛物线于![]() 两个不同的点,设
两个不同的点,设![]() .
.
(1)求抛物线的方程及椭圆的方程;
(2)若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)设椭圆的方程为![]() ,运用离心率公式和点满足椭圆方程,解方程可得
,运用离心率公式和点满足椭圆方程,解方程可得![]() ,进而得到椭圆的方程;再由焦点坐标可得
,进而得到椭圆的方程;再由焦点坐标可得![]() ,进而得到抛物线的方程;
,进而得到抛物线的方程;
(2)记![]() ,运用向量共线的坐标表示和联立直线方程和抛物线方程,运用韦达定理和弦长公式,及基本不等式,即可得到所求范围.
,运用向量共线的坐标表示和联立直线方程和抛物线方程,运用韦达定理和弦长公式,及基本不等式,即可得到所求范围.
(1)设椭圆的标准方程为![]() ,由题意得
,由题意得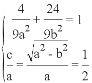 ,解得
,解得![]()
∴椭圆的方程为![]()
∴点![]() 的坐标为
的坐标为![]() ,∴
,∴![]() ,∴抛物线的方程是
,∴抛物线的方程是![]()
(2)由题意得直线![]() 的斜率存在,设其方程为
的斜率存在,设其方程为![]() ,
,
由![]() 消去
消去![]() 整理得
整理得![]() (*)∵直线
(*)∵直线![]() 与抛物线交于两点,∴
与抛物线交于两点,∴![]() ,设
,设![]() ,则
,则![]() ①,
①,![]() ②,
②,
∵![]() ,
,![]() ∴
∴![]() ∴
∴![]() ,③
,③
由①②③消去![]() 得
得![]() .
.
∴![]()
![]()
![]() ,即
,即![]()
![]() ,将
,将![]() 代入上式得,
代入上式得,![]()
![]() ,∵
,∵![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,即
,即![]() ,∴
,∴![]()
![]() ,
,
∴![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】已知下表为函数![]() 部分自変量取值及其对应函数值,为了便于研究,相关函数值取非整数值时,取值精确到0.01.
部分自変量取值及其对应函数值,为了便于研究,相关函数值取非整数值时,取值精确到0.01.
| 0.61 | -0.59 | -0.56 | -0.35 | 0 | 0.26 | 0.42 | 1.57 | 3.27 |
| 0.07 | 0.02 | -0.03 | -0.22 | 0 | 0.21 | 0.20 | -10.04 | -101.63 |
据表中数据,研究该函数的一些性质;
(1)判断函数![]() 的奇偶性,并证明;
的奇偶性,并证明;
(2)判断函数![]() 在区间[0.55,0.6]上是否存在零点,并说明理由;
在区间[0.55,0.6]上是否存在零点,并说明理由;
(3)判断![]() 的正负,并证明函数
的正负,并证明函数![]() 在
在![]() 上是单调递减函数.
上是单调递减函数.


