题目内容
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为矩形,且
为矩形,且![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)过点![]() 作一条射线
作一条射线![]() ,使得
,使得![]() ,求证:平面
,求证:平面![]()
![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值的绝对值.
的余弦值的绝对值.

【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)连线![]() 和
和![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() 是
是![]() 的中点,由中位线定理得
的中点,由中位线定理得![]() ,由线面平行的判定定理得以
,由线面平行的判定定理得以![]() 平面
平面![]() ;同理得
;同理得![]() 平面
平面![]() ,进而由面面平行得判定定理可得结论;(2)分别以
,进而由面面平行得判定定理可得结论;(2)分别以![]() ,
,![]() ,
,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系,分别求出平面
轴建立如图所示的空间直角坐标系,分别求出平面![]() 的一个法向量和平面
的一个法向量和平面![]() 的一个法向量,进而用空间向量夹角余弦公式求解.
的一个法向量,进而用空间向量夹角余弦公式求解.
试题解析:(1)证明:在矩形![]() 中,连线
中,连线![]() 和
和![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() 是
是![]() 的中点,由于
的中点,由于![]() 是
是![]() 的中点,所以
的中点,所以![]() 是△
是△![]() 的中位线,则
的中位线,则![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() ,同理得
,同理得![]() 平面
平面![]() ,
,
因为![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)解:分别以![]() ,
,![]() ,
,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系.
轴建立如图所示的空间直角坐标系.
设![]() ,则
,则![]() ,
,![]() ,故
,故![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则有
,则有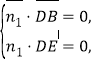 即
即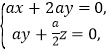 令
令![]() ,则
,则![]() ,
,![]() ,故
,故![]() .
.
同理,可得平面![]() 的一个法向量
的一个法向量![]() ,
,
所以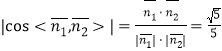 ,即二面角
,即二面角![]() 的余弦值的绝对值为
的余弦值的绝对值为![]() .
.

【题目】第![]() 届亚运会于
届亚运会于![]() 年
年![]() 月
月![]() 日至
日至![]() 日在中国广州进行,为了做好接待工作,组委会招募了
日在中国广州进行,为了做好接待工作,组委会招募了![]() 名男志愿者和
名男志愿者和![]() 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有![]() 人和
人和![]() 人喜爱运动,其余不喜爱.
人喜爱运动,其余不喜爱.
根据以上数据完成以下![]() 列联表:
列联表:
喜爱运动 | 不喜爱运动 | 总计 | |
男 | 10 | 16 | |
女 | 6 | 14 | |
总计 | 30 |
(2)能否在犯错误的概率不超过![]() 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关?
(3)如果从喜欢运动的女志愿者中(其中恰有![]() 人会外语),抽取
人会外语),抽取![]() 名负责翻译工作,则抽出的志愿者中
名负责翻译工作,则抽出的志愿者中![]() 人都能胜任翻译工作的概率是多少?
人都能胜任翻译工作的概率是多少?
附:K2=![]()
P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】某旅游为了解2015年国庆节期间参加某境外旅游线路的游客的人均购物消费情况,随机对50人做了问卷调查,得如下频数分布表:
人均购物消费情况 | [0,2000] | (2000,4000] | (4000,6000] | (6000,8000] | (8000,10000] |
额数 | 15 | 20 | 9 | 3 | 3 |
附:临界值表参考公式:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
(1)做出这些数据的频率分布直方图并估计次境外旅游线路游客的人均购物的消费平均值;
(2)在调查问卷中有一项是“您会资助失学儿童的金额?”,调查情况如表,请补全如表,并说明是否有95%以上的把握认为资助数额多于或少于500元和自身购物是否到4000元有关?
人均购物消费不超过4000元 | 人均购物消费超过4000元 | 合计 | |
资助超过500元 | 30 | ||
资助不超过500元 | 6 | ||
合计 |