题目内容
【题目】已知数列{an}的前n项和Sn=k3n﹣m,且a1=3,a3=27.
(I)求证:数列{an}是等比数列;
(II)若anbn=log3an+1 , 求数列{bn}的前n项和Tn .
【答案】证明:(I)∵ ![]() ,∴S1=a1=3k﹣m=3,a3=S3﹣S2=18k=27,解得
,∴S1=a1=3k﹣m=3,a3=S3﹣S2=18k=27,解得 ![]() .
.
则当n≥2时, ![]() ,
,
又a1=3,∴n∈N* , ![]() .
.
则 ![]() 为常数,故由等比数列的定义可知,数列{an}是等比数列.
为常数,故由等比数列的定义可知,数列{an}是等比数列.
(II)解:∵anbn=log3an+1 , ∴ ![]() .
.
则 ![]() ,
,
∴ ![]() ,
,
则 ![]() ,
,
即 ![]() (n∈N*)
(n∈N*)
【解析】(I)利用递推关系与等比数列的定义即可证明.(II)利用“错位相减法”、等比数列的求和公式即可得出.
【考点精析】关于本题考查的等比关系的确定和数列的前n项和,需要了解等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断;数列{an}的前n项和sn与通项an的关系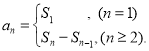 才能得出正确答案.
才能得出正确答案.

【题目】在某测试中,卷面满分为100分,60分为及格,为了调查午休对本次测试前两个月复习效果的影响,特对复习中进行午休和不进行午休的考生进行了测试成绩的统计,数据如下表所示:
分数段 | 29~ 40 | 41~ 50 | 51~ 60 | 61~ 70 | 71~ 80 | 81~ 90 | 91~ 100 |
午休考 生人数 | 23 | 47 | 30 | 21 | 14 | 31 | 14 |
不午休 考生人数 | 17 | 51 | 67 | 15 | 30 | 17 | 3 |
(1)根据上述表格完成列联表:
及格人数 | 不及格人数 | 总计 | |
午休 | |||
不午休 | |||
总计 |
(2)根据列联表可以得出什么样的结论?对今后的复习有什么指导意义?
【题目】某大学城校区与本部校区之间的驾车单程所需时间为![]() ,
,![]() 只与道路畅通状况有关,对其容量为500的样本进行统计,结果如下:
只与道路畅通状况有关,对其容量为500的样本进行统计,结果如下:
| 25 | 30 | 35 | 40 |
频数(次) | 100 | 150 | 200 | 50 |
以这500次驾车单程所需时间的频率代替某人1次驾车单程所需时间的概率.
(1)求![]() 的分布列与
的分布列与![]() ;
;
(2)某天有3位教师独自驾车从大学城校区返回本部校区,记![]() 表示这3位教师中驾车所用时间少于
表示这3位教师中驾车所用时间少于![]() 的人数,求
的人数,求![]() 的分布列与
的分布列与![]() ;
;
(3)下周某天张老师将驾车从大学城校区出发,前往本部校区做一个50分钟的讲座,结束后立即返回大学城校区,求张老师从离开大学城校区到返回大学城校区共用时间不超过120分钟的概率.