题目内容
【题目】定义在![]() 上的奇函数
上的奇函数![]() 有最小正周期
有最小正周期![]() ,且
,且![]() 时,
时,![]() .
.
(1)求![]() 在
在![]() 上的解析式;
上的解析式;
(2)判断![]() 在
在![]() 上的单调性,并给予证明;
上的单调性,并给予证明;
(3)当![]() 为何值时,关于方程
为何值时,关于方程![]() 在
在![]() 上有实数解?
上有实数解?
【答案】(1)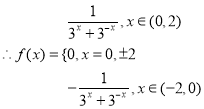 ;(2)
;(2)![]() 在
在![]() 单调递减;
单调递减;
(3)![]() 或
或![]() 或
或![]() .
.
【解析】
试题(1)可设![]() ,则
,则![]() ,由
,由![]() 时,
时,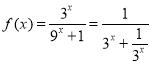 可求
可求![]() ,再由奇函数的性质可求
,再由奇函数的性质可求
(2)利用函数的单调性的定义进行证明即可
(3)转化为求解函数![]() 在
在![]() 上的值域,结合(2)可先求
上的值域,结合(2)可先求![]() 在
在![]() 上的值域,然后结合奇函数的对称性可求在
上的值域,然后结合奇函数的对称性可求在![]() 上的值域
上的值域
试题解析:(1)设![]() ,则
,则![]()
∵![]() 时,
时,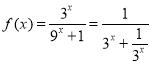 ,
,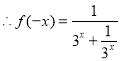
由函数![]() 为奇函数可得,
为奇函数可得,![]() ,∴
,∴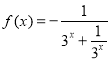 ,∵
,∵![]() ,
,
又因为函数是周期为4的为奇函数,![]() ,
,![]() ,
,
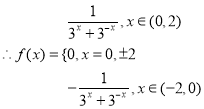
(2)设![]() ,令
,令![]() ,
,
则![]()
![]()
∵![]() ,∴
,∴![]() ,
,
∴函数![]() 在
在![]() 单调递增,且
单调递增,且![]() ,
,
∴![]() 在
在![]() 单调递减
单调递减
(3)由(2)可得当![]() 时,
时,![]() 单调递减,故
单调递减,故![]() ,
,
由奇函数的对称性可得,![]() 时,
时,![]()
当![]() 时,
时,![]()
∵关于方程![]() 在
在![]() 上有实数解,
上有实数解,![]() 或
或![]() 或
或![]()

 阅读快车系列答案
阅读快车系列答案【题目】某贫困地区共有1500户居民,其中平原地区1050户,山区450户.为调查该地区2017年家庭收入情况,从而更好地实施“精准扶贫”,采用分层抽样的方法,收集了150户家庭2017年年收入的样本数据(单位:万元).

(1)应收集多少户山区家庭的样本数据?
(2)根据这150个样本数据,得到2017年家庭收入的频率分布直方图(如图所示),其中样本数据分组区间为(0,0.5],(0.5,1],(1,1.5],(1.5,2],(2,2.5],(2.5,3].如果将频率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
(3)样本数据中,有5户山区家庭的年收入超过2万元,请完成2017年家庭收入与地区的列联表,并判断是否有90%的把握认为“该地区2017年家庭年收入与地区有关”?
超过2万元 | 不超过2万元 | 总计 | |
平原地区 | |||
山区 | 5 | ||
总计 |
附:
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |