题目内容
【题目】某校为扩大教学规模,从今年起扩大招生,现有学生人数为![]() 人,以后学生人数年增长率为
人,以后学生人数年增长率为![]() .该校今年年初有旧实验设备
.该校今年年初有旧实验设备![]() 套,其中需要换掉的旧设备占了一半.学校决定每年以当年年初设备数量的
套,其中需要换掉的旧设备占了一半.学校决定每年以当年年初设备数量的![]() 的增长率增加新设备,同时每年淘汰
的增长率增加新设备,同时每年淘汰![]() 套旧设备.
套旧设备.
(1)如果10年后该校学生的人均占有设备的比率正好比目前翻一番,那么每年应更换的旧设备是多少套?
(2)依照(1)的更换速度,共需多少年能更换所有需要更换的旧设备?
下列数据提供计算时参考:
|
|
|
|
|
|
【答案】(1)![]() 套;(2)16年
套;(2)16年
【解析】
(1)10年后学生人数为![]() ,设今年起学校的合格实验设备为数列
,设今年起学校的合格实验设备为数列![]() ,然后可得数列
,然后可得数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,然后求出
的等比数列,然后求出![]() 即可算出答案.
即可算出答案.
(2)根据(1)中的结果,直接算出即可
(1)今年学生人数为![]() 人,则10年后学生人数为
人,则10年后学生人数为![]() ,
,
设今年起学校的合格实验设备为数列![]()
则![]() ,
,![]()
令![]() ,则
,则![]()
所以![]() ,即
,即![]()
所以数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列
的等比数列
所以![]() ,即
,即![]()
所以![]()
由题意得![]() ,解得
,解得![]() .∴每年应更换的旧设备为
.∴每年应更换的旧设备为![]() 套.
套.
(2)全部更换旧设备共需![]() 年.
年.
答:(1)每年应更换的旧设备为![]() 套.
套.
(2)按此速度全部更换旧设备共需16年.

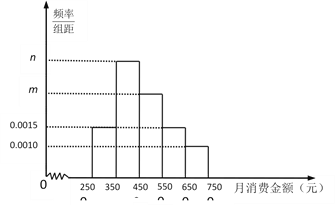
【题目】某机构为了解某地区中学生在校月消费情况,随机抽取了100名中学生进行调查.右图是根据调查的结果绘制的学生在校月消费金额的频率分布直方图.已知[350,450),[450,550),[550,650)三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群” .
(1)求m,n的值,并求这100名学生月消费金额的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)根据已知条件完成下面2×2列联表,并判断能否有90%的把握认为“高消费群”与性别有关?
高消费群 | 非高消费群 | 合计 | |
男 | |||
女 | 10 | 50 | |
合计 |
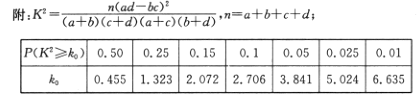
(参考公式:![]() ,其中
,其中![]() )
)
P( | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |