题目内容
19.已知数列{an}满足0<a1≠1,且an+1=$\frac{3{a}_{n}}{2{a}_{n}+1}$,(n∈N*).(1)求证:an+1≠an;
(2)若a1=$\frac{1}{3}$,求数列{an}的通项公式.
分析 (1)由已知条件推导出$\frac{1}{{a}_{n+1}}-1$=$\frac{1}{3}$($\frac{1}{{a}_{n}}-1$),从而得到an=$\frac{1}{1+\frac{1}{{3}^{n-1}}(\frac{1}{{a}_{1}}-1)}$,由此能证明an+1≠an.
(2)由{$\frac{1}{{a}_{n}}-1$}是公比为$\frac{1}{3}$的等比数列,a1=$\frac{1}{3}$,能过河卒子 同数列{an}的通项公式.
解答 (1)证明:∵数列{an}满足0<a1≠1,且an+1=$\frac{3{a}_{n}}{2{a}_{n}+1}$,(n∈N*),
∴$\frac{1}{{a}_{n+1}}$=$\frac{2{a}_{n}+1}{3{a}_{n}}$=$\frac{1}{3{a}_{n}}$+$\frac{2}{3}$,
∴$\frac{1}{{a}_{n+1}}-1$=$\frac{1}{3}$($\frac{1}{{a}_{n}}-1$),
∴{$\frac{1}{{a}_{n}}-1$}是公比为$\frac{1}{3}$的等比数列,
∴$\frac{1}{{a}_{n}}$-1=($\frac{1}{{a}_{1}}-1$)$•\frac{1}{{3}^{n-1}}$,
∴an=$\frac{1}{1+\frac{1}{{3}^{n-1}}(\frac{1}{{a}_{1}}-1)}$,
∵0<a1≠1,
∴an+1-an=$\frac{1}{1+{3}^{n}(\frac{1}{{a}_{1}}-1)}$-$\frac{1}{1+{3}^{n-1}(\frac{1}{{a}_{1}}-1)}$≠0,
∴an+1≠an.
(2)解:∵a1=$\frac{1}{3}$,
∴${a}_{n}=\frac{1}{1+\frac{1}{{3}^{n-1}}(\frac{1}{\frac{1}{3}}-1)}$=$\frac{{3}^{n-1}}{{3}^{n-1}+2}$=$\frac{{3}^{n}}{{3}^{n}+6}$.
∴数列{an}的通项公式an=$\frac{{3}^{n}}{{3}^{n}+6}$.
点评 本题考查数列中各项不相等的证明,考查数列的通项公式的求法,是中档题,解题时要认真审题,注意构造法的合理运用.

| A. | b=1,c=$\sqrt{2}$ | B. | b=$\sqrt{2}$,c=1 | C. | b=$\frac{\sqrt{2}}{2}$,c=1+$\frac{\sqrt{2}}{2}$ | D. | b=1+$\frac{\sqrt{2}}{2}$,c=$\frac{\sqrt{2}}{2}$ |
| A. | 第一、二象限 | B. | 第三、四象限 | ||
| C. | 第一、四象限 | D. | 第二、三象限或x负半轴或y轴 |
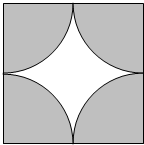 某铝制品厂在边长为40cm的正方形铝板上割下四个半径为20厘米的圆形(如图所示的阴影部分).该厂打算用余下的部分制作底面直径和高相等的圆柱形包装盒(接缝用料忽略不计).问:
某铝制品厂在边长为40cm的正方形铝板上割下四个半径为20厘米的圆形(如图所示的阴影部分).该厂打算用余下的部分制作底面直径和高相等的圆柱形包装盒(接缝用料忽略不计).问: