题目内容
【题目】定义:从数列![]() 中抽取
中抽取![]() 项按其在
项按其在![]() 中的次序排列形成一个新数列
中的次序排列形成一个新数列![]() ,则称
,则称![]() 为
为![]() 的子数列;若
的子数列;若![]() 成等差(或等比),则称
成等差(或等比),则称![]() 为
为![]() 的等差(或等比)子数列.
的等差(或等比)子数列.
(1)记数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() .
.
①求数列![]() 的通项公式;
的通项公式;
②数列![]() 是否存在等差子数列,若存在,求出等差子数列;若不存在,请说明理由.
是否存在等差子数列,若存在,求出等差子数列;若不存在,请说明理由.
(2)已知数列![]() 的通项公式为
的通项公式为![]() ,证明:
,证明:![]() 存在等比子数列.
存在等比子数列.
【答案】(1)①![]() ;②见解析;(2)见证明
;②见解析;(2)见证明
【解析】
(1)①先由![]() 得到
得到![]() ,再由
,再由![]() 得到通项公式,进而可得出结果;
得到通项公式,进而可得出结果;
②假设从数列![]() 中抽3项
中抽3项![]() 成等差,则
成等差,则![]() ,根据等差子数列的概念,即可得出结论;
,根据等差子数列的概念,即可得出结论;
(2)先假设数列![]() 中存在3项
中存在3项![]() ,
,![]() ,
,![]() 成等比.设
成等比.设![]() ,则
,则![]() ,故可设
,故可设![]() (
(![]() 与
与![]() 是互质的正整数).根据题意,得到需要
是互质的正整数).根据题意,得到需要![]() ,再由题中等比子数列的概念,即可得出结论.
,再由题中等比子数列的概念,即可得出结论.
解:(1)①因为![]() ,所以当
,所以当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() .
.
综上可知:![]() .
.
②假设从数列![]() 中抽3项
中抽3项![]() 成等差,
成等差,
则![]() ,即
,即![]() ,
,
化简得:![]() .
.
因为![]() ,所以
,所以![]() ,
,![]() ,且
,且![]() ,
,![]() 都是整数,
都是整数,
所以![]() 为偶数,
为偶数,![]() 为奇数,所以
为奇数,所以![]() 不成立.
不成立.
因此,数列![]() 不存在三项等差子数列.
不存在三项等差子数列.
若从数列![]() 中抽
中抽![]() 项,其前三项必成等差数列,不成立.
项,其前三项必成等差数列,不成立.
综上可知,数列![]() 不存在等差子数列.
不存在等差子数列.
(2)假设数列![]() 中存在3项
中存在3项![]() ,
,![]() ,
,![]() 成等比.
成等比.
设![]() ,则
,则![]() ,故可设
,故可设![]() (
(![]() 与
与![]() 是互质的正整数).
是互质的正整数).
则需满足![]() ,
,
即需满足![]() ,则需满足
,则需满足![]() .
.
取![]() ,则
,则![]() .
.
此时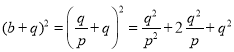 ,
,
![]() .
.
故此时![]() 成立.
成立.
因此数列![]() 中存在3项
中存在3项![]() ,
,![]() ,
,![]() 成等比,
成等比,
所以数列![]() 存在等比子数列.
存在等比子数列.

 探究与巩固河南科学技术出版社系列答案
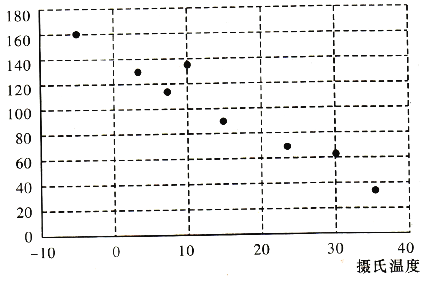
探究与巩固河南科学技术出版社系列答案【题目】有一个同学家开了一个小卖部,他为了研究气温对热饮饮料销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的散点图和对比表:
摄氏温度 |
|
|
|
|
|
|
|
|
热饮杯数 |
|
|
|
|
|
|
|
|
(1)从散点图可以发现,各点散布在从左上角到右下角的区域里。因此,气温与当天热饮销售杯数之间成负相关,即气温越高,当天卖出去的热饮杯数越少。统计中常用相关系数![]() 来衡量两个变量之间线性关系的强弱.统计学认为,对于变量
来衡量两个变量之间线性关系的强弱.统计学认为,对于变量![]() 、
、![]() ,如果
,如果![]() ,那么负相关很强;如果
,那么负相关很强;如果![]() ,那么正相关很强;如果
,那么正相关很强;如果![]() ,那么相关性一般;如果
,那么相关性一般;如果![]() ,那么相关性较弱。请根据已知数据,判断气温与当天热饮销售杯数相关性的强弱.
,那么相关性较弱。请根据已知数据,判断气温与当天热饮销售杯数相关性的强弱.
(2)(i)请根据已知数据求出气温与当天热饮销售杯数的线性回归方程;
(ii)记![]() 为不超过
为不超过![]() 的最大整数,如
的最大整数,如![]() ,
,![]() .对于(i)中求出的线性回归方程
.对于(i)中求出的线性回归方程![]() ,将
,将![]() 视为气温与当天热饮销售杯数的函数关系.已知气温
视为气温与当天热饮销售杯数的函数关系.已知气温![]() 与当天热饮每杯的销售利润
与当天热饮每杯的销售利润![]() 的关系是
的关系是![]()
![]() (单位:元),请问当气温
(单位:元),请问当气温![]() 为多少时,当天的热饮销售利润总额最大?
为多少时,当天的热饮销售利润总额最大?
(参考公式)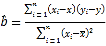 ,
,![]() ,
,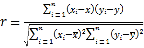
(参考数据)![]() ,
,![]() ,
,![]()
![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
【题目】甲、乙两人参加一个射击的中奖游戏比赛,在相同条件下各打靶50次,统计每次打靶所得环数,得下列频数分布表.
环数 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲的频数 | 0 | 1 | 4 | 7 | 14 | 16 | 6 | 2 |
乙的频数 | 1 | 2 | 5 | 6 | 10 | 16 | 8 | 2 |
比赛中规定所得环数为1,2,3,4时获奖一元,所得环数为5,6,7时获奖二元,所得环数为8,9时获奖三元,所得环数为10时获奖四元,没命中则无奖.
(1)根据上表,在答题卡给定的坐标系内画出甲射击50次获奖金额(单位:元)的条形图;

(2)估计甲射击1次所获奖至少为三元的概率;
(3)要从甲、乙两人中选拔一人参加射击比赛,请你根据甲、乙两人所获奖金额的平均数和方差作出选择.