题目内容
【题目】如图1,矩形![]() 中,
中,![]() ,
,![]() 是
是![]() 边上异于端点的动点,
边上异于端点的动点,![]() ,将矩形
,将矩形![]() 沿
沿![]() 折叠至
折叠至![]() 处,使面
处,使面![]() (如图2).点
(如图2).点![]() 满足
满足![]() ,
,![]() .
.
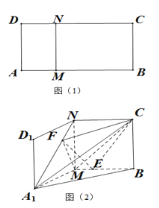
(1)证明:![]() ;
;
(2)设![]() ,当
,当![]() 为何值时,四面体
为何值时,四面体![]() 的体积最大,并求出最大值.
的体积最大,并求出最大值.
【答案】(1)见证明;(2)当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
【解析】
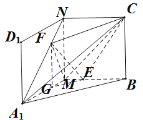
(1)在面![]() 内,过点F作FG
内,过点F作FG![]() 交
交![]() 于点G,连接GE.根据线线平行得
于点G,连接GE.根据线线平行得
![]() 面
面![]() 及
及![]() 面
面![]() ,从而得到面
,从而得到面![]() 面
面![]() ,可证得结论;
,可证得结论;
(2)![]() ,则BM=2-x,ME=
,则BM=2-x,ME=![]() GM=
GM=![]() ,可证
,可证![]() 面MEC,得
面MEC,得![]() ,
,![]() ,由二次函数求得最值即可.
,由二次函数求得最值即可.
(1)在面![]() 内,过点F作FG
内,过点F作FG![]() 交
交![]() 于点G,连接GE.
于点G,连接GE.
![]() ,
,![]() ,又
,又![]() 面
面![]() ,FG
,FG![]() 面
面![]()
![]() 面
面![]() .
.
由![]() 得
得![]() ,同理可证得
,同理可证得![]() 面
面![]() .
.
又![]() ,
,![]() 面
面![]() ,
,
∴面![]() 面
面![]() ,
,
又![]() 面
面![]() ,
,
![]() 面
面![]()
(2)![]() ,则BM=2-x,ME=
,则BM=2-x,ME=![]() GM=
GM=![]() ,
,
面![]() 面MBCN,面
面MBCN,面![]() 面MBCN=NM,
面MBCN=NM,
![]() 面
面![]() ,
,
![]() 则
则![]() 面MBCN,即
面MBCN,即![]() 面MEC,
面MEC,
又GF![]() 面MEC,
面MEC,
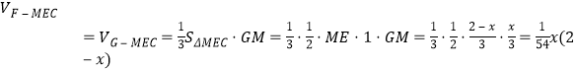 ,
,![]()
当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.

练习册系列答案
相关题目