Question

【题目】试问:能否把2008表示成的形式?如果可以,这种表示方式是否有无限多个?其中,m、n均为大于100且小于170的正整数,且;均为两两不相等的小于6的正有理数,且均为大于1且小于5的正整数,同时, 两两不相等,也两两不相等请说明理由.

Answer 1

【答案】见解析

【解析】

满足题目要求的表示方式是存在的，且有无限多个.理由如下.

为方便计，试取，考虑和式

.①

注意到

，

则.②

由式①、②得

.

故

.

则

，

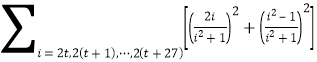这里（的取法有无限多个，表示式也有无限多个）.

正项共有110+28×2=166个，而负项共有110个，均为两两不等的小于6的正有理数.

（注意到，因为为偶数；又与互质， 与互质，也是因为为偶数；另外，，因为），从而，两两不相等.

显然满足“大于100且小于170，”.

另外，也容易验证：以上的表示方式都满足“也两两不相等”.

综上所述，以上所构造的2008的表示式完全符合题目要求，且表示式有无限多个.