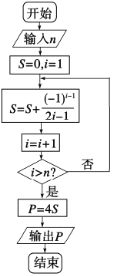
题目内容
【题目】已知函数f（x）＝（1﹣sinx）ex.
（1）求f（x）在区间（0，π）的极值；
（2）证明：函数g（x）＝f（x）﹣sinx﹣1在区间（﹣π，π）有且只有3个零点，且之和为0.
【答案】（1）极小值
，无极大值；（2）见解析
【解析】
（1）先对函数进行求导，再根据导函数的零点进行分类讨论即可；
（2）先求出0是
的一个零点，然后判断出
在
上的单调性，结合第（1）问，得出在上的单调性，进而得出在只有一个零点
；通过求
，可以得到在
上也只有一个零点
；从而证明函数在区间
有且只有3个零点，且之和为0.
（1）因为
，
所以
，
令
，得
，
，从而
，
当
时，
，
，
所以
，
，从而
单调递减；
当
，
，
，
所以
，
，从而单调递增，
故在区间有极小值，无极大值；
（2）证明：因为
，所以
，从而
是
的一个零点；
令，则
在区间
单调递减，在区间
单调递增，
所以在区间单调递减，在区间单调递增，
又
，
，
所以在区间有唯一的零点，记为，
又因为
，
所以对于任意的
，若
，必有
，
所以在区间有唯一的零点，
故在区间的零点为，0，，
所以在区间有且只有3个零点，且之和为0.
【题目】某大型超市抽查了100天该超市的日纯利润数据，并将日纯利润数据分成以下几组（单位：万元）：
，
，
，
，
，
，统计结果如下表所示：
组别 |
|
|
|
|
|
|
频数 | 5 | 20 | 30 | 30 | 10 | 5 |
以上述样本分布的频率估计总体分布的概率，解决下列问题：
（1）从该大型超市近几年的销售记录中抽出5天，求其中日纯利润在区间
内的天数不少于2的概率；
（2）该超市经理由频数分布表可以认为，该大型超市每天的纯利润
服从正态分布
，其中，
近似为样本平均数
（每组数据取区间的中点值）.
①试利用该正态分布，估计该大型超市1000天内日纯利润在区间
内的天数（精确到个位）；
②该大型超市负责人根据每日的纯利润给超市员工制定了两种不同的奖励方案：
方案一：直接发放奖金，日纯利润低于时每名员工发放奖金70元，日纯利润不低于时每名员工发放奖金90元；
方案二：利用抽奖的方式获得奖金，其中日纯利润不低于时每位员工均有两次抽奖机会，日纯利润低于时每位员工只有一次抽奖机会；每次抽奖的奖金及对应的概率分别为
金额 | 50元 | 100元 |
概率 |
|
|
小张恰好为该大型超市的一名员工，则从数学期望的角度看，小张选择哪种奖励方案更有利？
参考数据：若
，则
，
.
