题目内容
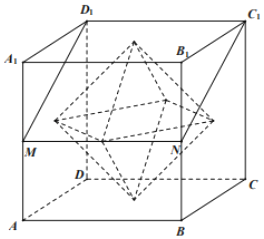
【题目】如图,点M,N分别为正方体ABCD﹣A1B1C1D1的棱AA1,BB1的中点,以正方体的六个面的中心为顶点构成一个八面体,若平面D1MNC1将该八面体分割成上、下两部分的体积分别为V1、V2,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
如图,先作出平面![]() 截八面体的截面为
截八面体的截面为![]() ,建立空间直角坐标系,用点
,建立空间直角坐标系,用点![]() 到平面
到平面![]() 的距离
的距离![]() 为向量
为向量![]() 在法向量
在法向量![]() 上的投影的长,再计算两部分的体积,得到体积之比,得到答案.
上的投影的长,再计算两部分的体积,得到体积之比,得到答案.
正方体的六个面的中心为顶点构成的八面体中中间和上方的顶点分别为![]()
如图,分别过![]() 作侧棱的平行线,
作侧棱的平行线,
分别![]() 交于点
交于点![]() ,分别
,分别![]() 交于点
交于点![]() ,得到矩形
,得到矩形![]() .
.

由题意有![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
在矩形![]() 中,
中,![]() 分别交
分别交![]() 于点
于点![]() ,则
,则![]() 分别为
分别为![]() 的中点,
的中点,
![]() 平面
平面![]() ,所以,
,所以,![]() 平面
平面![]() .
.
将平面![]() 延展与
延展与![]() 交于
交于![]() 点. 所以平面
点. 所以平面![]() 截八面体的截面为
截八面体的截面为![]() .
.
显然![]() 与
与![]() 相交于
相交于![]() 的中点,设为
的中点,设为![]() .则
.则![]() 三点共线.
三点共线.
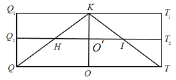
在![]() 中,过
中,过![]() 作
作![]() ,如图,可得
,如图,可得![]() 为
为![]() 的一个三等分点.
的一个三等分点.

设正方体的棱长为2,则![]() .
.
以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系
P(-1,0,0),R(1,0,0),Q(0,-1,0),
![]()
![]()
![]()
设平面![]() 的法向量为
的法向量为![]() .
.
则 ,即
,即 ,取
,取![]() 则
则![]()
则点![]() 到平面
到平面![]() 的距离
的距离![]() 为向量
为向量![]() 在法向量
在法向量![]() 上的投影的长.
上的投影的长.
所以
又![]()

![]()
![]()
所以八面体在平面平面![]() 下方的部分的体积为
下方的部分的体积为![]()
所以![]()
故选:A


练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目