题目内容
【题目】已知抛物线G:x2=2py(p>0),直线y=k(x﹣1)+2与抛物线G相交A(x1 , y1),B(x2 , y2)(x1<x2),过A,B点分别作抛物线G的切线L1 , L2 , 两切线L1 , L2相交H(x,y),
(1)若k=1,有 L1⊥L2 , 求抛物线G的方程;
(2)若p=2,△ABH的面积为S1 , 直线AB与抛物线G围成封闭图形的面积为S2 , 证明: ![]() 为定值.
为定值.
【答案】
(1)
解:x2=2py(p>0),即y= ![]() ,
,
导数为y′= ![]() ,切线L1,L2的斜率分别为
,切线L1,L2的斜率分别为 ![]() ,
, ![]() ,
,
L1⊥L2,可得 ![]()
![]() =﹣1,
=﹣1,
联立直线y=x+1和x2=2py(p>0),
可得x2﹣2px﹣2p=0,即有x1x2=﹣2p,
即有﹣p2=﹣2p,解得p=2,
则抛物线G的方程为x2=4y;
(2)
解:证明:将直线y=k(x﹣1)+2代入抛物线方程x2=4y,
可得x2﹣4kx+4k﹣8=0,
即有x1+x2=4k,x1x2=4k﹣8,
x1<x2,可得x2﹣x1= ![]() =
= ![]() =4
=4 ![]() .
.
抛物线的方程为y= ![]() x2,求导得y′=
x2,求导得y′= ![]() x,
x,
过抛物线上A、B两点的切线方程分别是y﹣y1= ![]() x1(x﹣x1),y﹣y2=
x1(x﹣x1),y﹣y2= ![]() x2(x﹣x2),
x2(x﹣x2),
即y= ![]() x1x﹣
x1x﹣ ![]() x12,y=
x12,y= ![]() x2x﹣
x2x﹣ ![]() x22,
x22,
解得两条切线l1、l2的交点H的坐标为( ![]() ,
, ![]() ),即H(2k,k﹣2).
),即H(2k,k﹣2).
可得H到直线y=k(x﹣1)+2的距离为d= ![]() =
= ![]() ,
,
|AB|= ![]() |x2﹣x1|=4
|x2﹣x1|=4 ![]()
![]() .
.
可得△ABH的面积为S1= ![]() d|AB|=
d|AB|= ![]()
![]() 4
4 ![]()
![]()
=4(k2﹣k+2) ![]() .
.
直线AB与抛物线G围成封闭图形的面积为S2= ![]() [k(x﹣1)+2﹣
[k(x﹣1)+2﹣ ![]() x2]dx
x2]dx
=[ ![]() kx2+(2﹣k)x﹣
kx2+(2﹣k)x﹣ ![]() x3]|
x3]| ![]() =
= ![]() k(x2﹣x1)(x2+x1)+(2﹣k)(x2﹣x1)﹣
k(x2﹣x1)(x2+x1)+(2﹣k)(x2﹣x1)﹣ ![]() (x2﹣x1)[(x2+x1)2﹣x1x2]
(x2﹣x1)[(x2+x1)2﹣x1x2]
=(x2﹣x1)[2k2+2﹣k﹣ ![]() (16k2﹣4k+8)]=4
(16k2﹣4k+8)]=4 ![]()
![]() (k2﹣k+2)=
(k2﹣k+2)= ![]() (k2﹣k+2)
(k2﹣k+2) ![]() .
.
则 ![]() 为定值
为定值 ![]()
【解析】(1)求出函数y= ![]() 的导数,可得切线的斜率,由两直线垂直的条件:斜率之积为﹣1,再将直线y=x+1代入抛物线方程,运用韦达定理,解方程可得p的值,进而得到抛物线的方程;(2)将直线y=k(x﹣1)+2代入抛物线方程x2=4y,运用韦达定理和弦长公式,求得|AB|,再由切线的方程求出交点H的坐标,运用点到直线的距离公式,结合三角形的面积公式可得S1, 再由直线AB与抛物线G围成封闭图形的面积为S2=
的导数,可得切线的斜率,由两直线垂直的条件:斜率之积为﹣1,再将直线y=x+1代入抛物线方程,运用韦达定理,解方程可得p的值,进而得到抛物线的方程;(2)将直线y=k(x﹣1)+2代入抛物线方程x2=4y,运用韦达定理和弦长公式,求得|AB|,再由切线的方程求出交点H的坐标,运用点到直线的距离公式,结合三角形的面积公式可得S1, 再由直线AB与抛物线G围成封闭图形的面积为S2= ![]() [k(x﹣1)+2﹣
[k(x﹣1)+2﹣ ![]() x2]dx,化简计算即可得到面积的比值为定值.
x2]dx,化简计算即可得到面积的比值为定值.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一人答一份).现从回收的年龄在2060岁的问卷中随机抽取了100份, 统计结果如下面的图表所示.
年龄 分组 | 抽取份 数 | 答对全卷的人数 | 答对全卷的人数占本组的概率 |
[20,30) | 40 | 28 | 0.7 |
[30,40) | n | 27 | 0.9 |
[40,50) | 10 | 4 | b |
[50,60] | 20 | a | 0.1 |
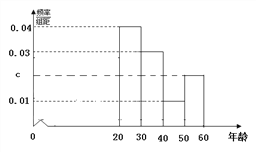
(1)分别求出n, a, b, c的值;
(2)从年龄在[40,60]答对全卷的人中随机抽取2人授予“环保之星”,求年龄在[50,60] 的人中至少有1人被授予“环保之星”的概率.
【题目】对某班一次测验成绩进行统计,如下表所示:
分数段 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
概率 | 0.02 | 0.04 | 0.17 | 0.36 | 0.25 | 0.15 |
(1)求该班成绩在[80,100]内的概率;
(2)求该班成绩在[60,100]内的概率.