题目内容
【题目】平面内一个整点的有限集
称为一个双邻集，如果对内每个点
，恰有点
、
、
、
中的两点在内.问对怎样的正整数
，存在一个双邻集恰包含个整点?
【答案】
和
（偶数）
.
【解析】
先证明结论：
一个双邻集
恰包含个整点，则必为偶数.将横纵坐标中一个相同，另一个相差1的两整点叫作互为相邻整点.用线段连结中的相邻整点.因为中每一整点恰连出两条线段，因此，双邻集内全部整点可用连结相邻整点的线段组成有限个不自交的闭折线图形.
在每一闭折线图形中，每两个相邻整点的横纵坐标之和只相差1，横纵坐标之和依次为偶数、奇数、偶数、奇数、……，交替出现.由于是闭折线，则任一个闭折线图形整点个数必为偶数个.
再证：和（偶数）.
当
时，2个整点显然无法构成一个双邻集.
当
时，由于3个及3个以下的整点无法组
成闭折线图形，则6个整点要成为一个双邻集，6个点组成的闭折线图形只能是图5所示的两图形之一.
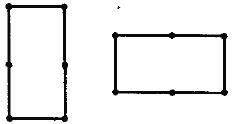
图中两图形显然都不是双邻集.
4个整点
、
、
、
恰组成一个双邻集（边长为1的正方形），则.
注意到10个整点、、
、
、、
、
、
、
、
也组成一个双邻集（长为3宽为2的矩形边上的10个整点）.
因此，当
时，取
个4整点组成的双邻集，每两个双邻集的距离（一个相邻集中任一点到另一双邻集中任一点距离的最小值）大于1，将这个4整点双邻集合并为一个集合，这个集合当然是恰含4个整点的双邻集.
当
时，由于
，取
个4整点组成的双邻集，取一个10整点组成的双邻集，每两个双邻集的距离大于1.将这个4整点双邻集与一个10整点双邻集合并为一个集合，这个集合当然是恰含
个整点的双邻集.
因此，和（偶数）.
练习册系列答案
相关题目
