题目内容
若存在正实数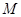 ,对于任意
,对于任意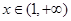 ,都有
,都有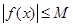 ,则称函数
,则称函数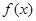 在
在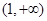 上是有
上是有
界函数.下列函数①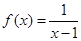 ; ②
; ②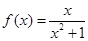 ; ③
; ③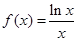 ; ④
; ④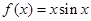 ,
,
其中“在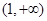 上是有界函数”的序号为 .
上是有界函数”的序号为 .
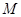 ,对于任意
,对于任意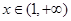 ,都有
,都有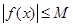 ,则称函数
,则称函数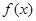 在
在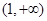 上是有
上是有界函数.下列函数①
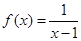 ; ②
; ②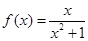 ; ③
; ③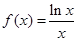 ; ④
; ④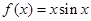 ,
,其中“在
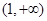 上是有界函数”的序号为 .
上是有界函数”的序号为 .②③
试题分析:因为
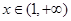 时,
时,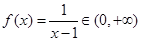 ,所以函数①不是有界函数.因为
,所以函数①不是有界函数.因为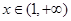 时,
时,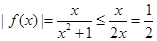 ,所以函数②是有界函数.因为
,所以函数②是有界函数.因为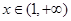 时,
时,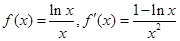 ,
,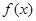 在
在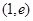 单调增,在
单调增,在 上单调减,所以函数
上单调减,所以函数 ,因此③是有界函数.因为
,因此③是有界函数.因为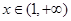 时,取
时,取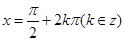 ,则
,则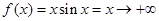 ,所以函数④不是有界函数.
,所以函数④不是有界函数.
练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 x3-ax+1.
x3-ax+1. .
.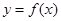 在
在 处的切线与直线
处的切线与直线 平行,求a的值;
平行,求a的值; 时,求
时,求 的单调区间.
的单调区间. 上可导的任意函数
上可导的任意函数 ,若满足
,若满足 ,则必有( ).
,则必有( ).


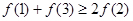
 :
:
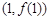 处的切线方程;
处的切线方程; 平行的曲线C的切线方程.
平行的曲线C的切线方程.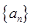 满足
满足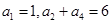 ,且对任意
,且对任意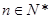 ,函数
,函数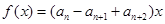
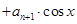
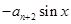 满足
满足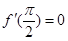 ,若
,若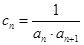 ,则数列
,则数列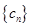 的前
的前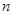 项和
项和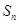 为 .
为 . 上的点
上的点 的切线平行于直线
的切线平行于直线 ,则切点
,则切点 或
或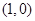

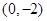 或
或 或
或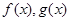 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当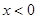 时
时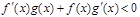 且
且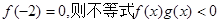 的解集为( )
的解集为( )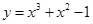 在点
在点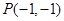 处的切线方程是
处的切线方程是