题目内容
已知双曲线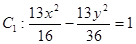 ,点
,点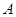 、
、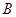 分别为双曲线
分别为双曲线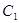 的左、右焦点,动点
的左、右焦点,动点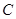 在
在 轴上方.
轴上方.
(1)若点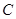 的坐标为
的坐标为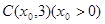 是双曲线的一条渐近线上的点,求以
是双曲线的一条渐近线上的点,求以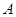 、
、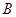 为焦点且经过点
为焦点且经过点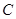 的椭圆的方程;
的椭圆的方程;
(2)若∠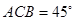 ,求△
,求△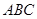 的外接圆的方程;
的外接圆的方程;
(3)若在给定直线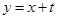 上任取一点
上任取一点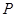 ,从点
,从点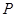 向(2)中圆引一条切线,切点为
向(2)中圆引一条切线,切点为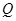 . 问是否存在一个定点
. 问是否存在一个定点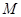 ,恒有
,恒有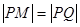 ?请说明理由.
?请说明理由.
(1)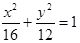 (2)
(2)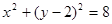 (3)存在
(3)存在
解析试题分析:(1)双曲线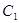 的左、右焦点
的左、右焦点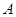 、
、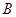 的坐标分别为
的坐标分别为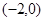 和
和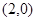 ,
,
∵双曲线的渐进线方程为: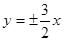 ,
,
∴点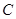 的坐标为
的坐标为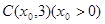 是渐进线
是渐进线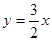 上的点,即点
上的点,即点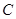 的坐标为
的坐标为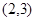 。
。
∵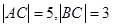 ∴椭圆的长轴长
∴椭圆的长轴长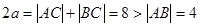
∵半焦距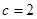 ,∴椭圆的方程
,∴椭圆的方程 ..5分
..5分
(2)∵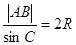 ,∴
,∴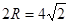 ,即
,即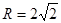
又圆心在线段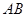 的垂直平分线上,故可设圆心
的垂直平分线上,故可设圆心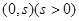
由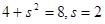 。∴△
。∴△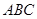 的外接圆的方程为
的外接圆的方程为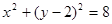 ..9分
..9分
(3)假设存在这样的定点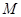
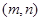 设点P的坐标为
设点P的坐标为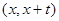
∵恒有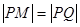 ,∴
,∴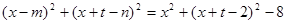
即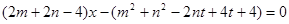 对
对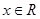 恒成立。
恒成立。
从而 ,消去
,消去 ,得
,得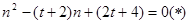
∵方程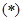 的判别式
的判别式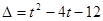
∴①当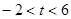 时,方程
时,方程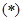 无实数解,∴不存在这样的定点
无实数解,∴不存在这样的定点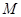 ;
;
②当 时,方程
时,方程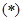 有实数解,此时
有实数解,此时 ,即直线
,即直线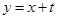 与圆相离或相切,故此时存在这样的定点
与圆相离或相切,故此时存在这样的定点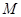 ; 14分
; 14分
考点:本题考查了圆锥曲线方程的求法及直线与圆的位置关系
点评:解析几何综合题主要考查直线和圆锥曲线的位置关系以及范围、最值、定点、定值、存在性等问题,直线与多种曲线的位置关系的综合问题将会逐步成为今后命题的热点,尤其是把直线和圆的位置关系同本部分知识的结合,将逐步成为今后命题的一种趋势

练习册系列答案
相关题目
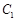 的极坐标方程是
的极坐标方程是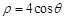 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴正方向建立平面直角坐标系,直线的参数方程是:
轴正方向建立平面直角坐标系,直线的参数方程是: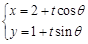 (为参数).
(为参数). ,
,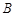 两点,点
两点,点 的直角坐标为
的直角坐标为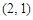 ,若
,若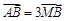 ,求直线的普通方程.
,求直线的普通方程.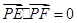 ,由点P向x轴作垂线段PQ,垂足为Q,点M满足
,由点P向x轴作垂线段PQ,垂足为Q,点M满足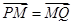 ,点M的轨迹为C.
,点M的轨迹为C. 与曲线C交于A、B两点,点N满足
与曲线C交于A、B两点,点N满足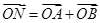
 过点
过点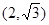 ,且它的离心率
,且它的离心率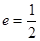 .直线
.直线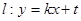 与椭圆
与椭圆 交于
交于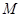 、
、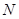 两点.
两点.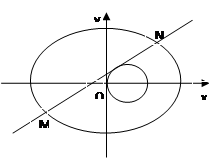
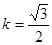 时,求证:
时,求证: 与圆
与圆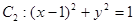 相切,椭圆上一点
相切,椭圆上一点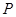 满足
满足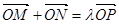 ,求实数
,求实数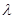 的取值范围.
的取值范围.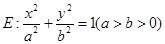 的右焦点
的右焦点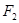 与抛物线
与抛物线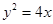 的焦点重合,过
的焦点重合,过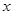 轴垂直的直线与椭圆交于
轴垂直的直线与椭圆交于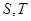 ,而与抛物线交于
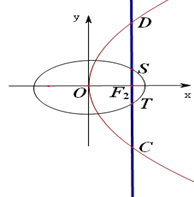
,而与抛物线交于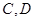 两点,且
两点,且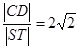 .
.
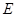 的方程;
的方程; 的直线与椭圆
的直线与椭圆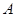 和
和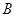 ,
, 为椭圆
为椭圆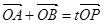 (
(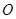 为坐标原点),求实数
为坐标原点),求实数 的取值范围.
的取值范围. .
.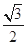 ,求椭圆的标准方程;
,求椭圆的标准方程;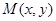 与两个定点
与两个定点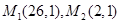 的距离之比等于5.
的距离之比等于5.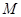 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形; ,过点
,过点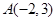 的直线
的直线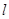 被
被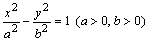 的右顶点为A,右焦点为F,右准线与
的右顶点为A,右焦点为F,右准线与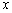 轴交于点B,且与一条渐近线交于点C,点O为坐标原点,
轴交于点B,且与一条渐近线交于点C,点O为坐标原点, ,
,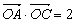 ,过点F的直线
,过点F的直线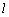 与双曲线右支交于点
与双曲线右支交于点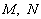 .
.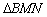 面积的最小值.
面积的最小值.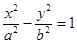 的离心率为2,焦点与椭圆
的离心率为2,焦点与椭圆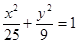 的焦点相同,求双曲线的方程及焦点坐标。
的焦点相同,求双曲线的方程及焦点坐标。