题目内容
已知椭圆 过点
过点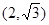 ,且它的离心率
,且它的离心率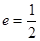 .直线
.直线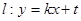 与椭圆
与椭圆 交于
交于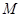 、
、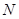 两点.
两点.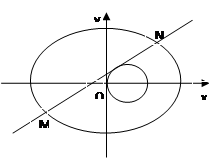
(Ⅰ)求椭圆的标准方程;
(Ⅱ)当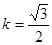 时,求证:
时,求证: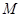 、
、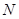 两点的横坐标的平方和为定值;
两点的横坐标的平方和为定值;
(Ⅲ)若直线 与圆
与圆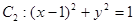 相切,椭圆上一点
相切,椭圆上一点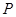 满足
满足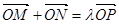 ,求实数
,求实数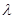 的取值范围.
的取值范围.
(Ⅰ)  ;
;
(Ⅱ)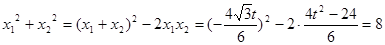 ,为定值.
,为定值.
(Ⅲ)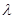 的取值范围为
的取值范围为 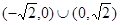 .
.
解析试题分析:(Ⅰ) 设椭圆的标准方程为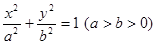
由已知得: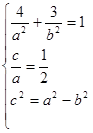 ,解得
,解得 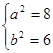
所以椭圆的标准方程为: 4分
4分
(Ⅱ) 由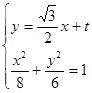 ,得
,得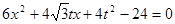 ,设
,设 ,
, ,
,
则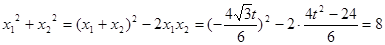 ,为定值. 9分
,为定值. 9分
(Ⅲ)因为直线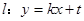 与圆
与圆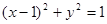 相切
相切
所以,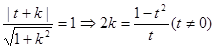
把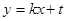 代入
代入 并整理得:
并整理得: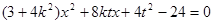
设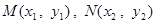 ,则有
,则有 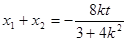
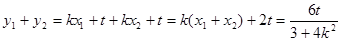
因为, , 所以,
, 所以,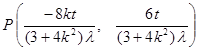
又因为点 在椭圆上, 所以,
在椭圆上, 所以,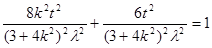
 . 因为
. 因为 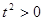 所以
所以 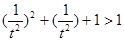 ,
,
所以 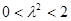 ,所以
,所以 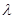 的取值范围为
的取值范围为 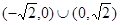 . 16分
. 16分
考点:本题主要考查椭圆的标准方程,椭圆的几何性质,直线与圆、椭圆的位置关系,二次函数性质。
点评:中档题,涉及椭圆的题目,在近些年高考题中是屡见不鲜,往往涉及求标准方程,研究直线与椭圆的位置关系。求标准方程,主要考虑定义及a,b,c,e的关系,涉及直线于椭圆位置关系问题,往往应用韦达定理。涉及直线于圆的位置关系问题,往往利用“特征三角形”。本题在应用韦达定理的基础上,得到参数的表达式,应用二次函数性质使问题得解。

练习册系列答案
相关题目
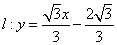 过双曲线
过双曲线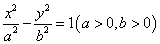 的一个焦点,且与双曲线的一条渐近线平行.
的一个焦点,且与双曲线的一条渐近线平行. 与
与 轴不平行的直线与双曲线相交于不同的两点
轴不平行的直线与双曲线相交于不同的两点 的垂直平分线为
的垂直平分线为 ,求直线
,求直线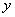 轴上截距的取值范围.
轴上截距的取值范围.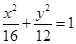 上找一点,使这一点到直线
上找一点,使这一点到直线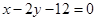 的距离的最小值
的距离的最小值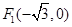 ,
,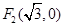 ,过
,过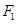 且与坐标轴不平行的直线
且与坐标轴不平行的直线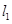 与椭圆交于
与椭圆交于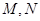 两点,如果
两点,如果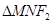 的周长等于8。
的周长等于8。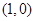 的直线
的直线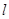 与椭圆交于不同两点
与椭圆交于不同两点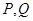 ,试问在
,试问在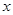 轴上是否存在定点
轴上是否存在定点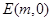 ,使
,使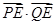 恒为定值?若存在,求出点
恒为定值?若存在,求出点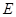 的坐标及定值;若不存在,说明理由。
的坐标及定值;若不存在,说明理由。 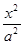 +
+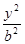 =1(a>b>0)的左、右焦点分别为F
=1(a>b>0)的左、右焦点分别为F 、F
、F ,A是椭圆C上的一点,AF
,A是椭圆C上的一点,AF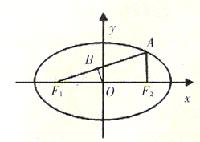
 +y
+y ,y
,y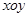 中,曲线
中,曲线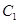 的参数方程为
的参数方程为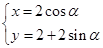 (
(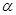 为参数)
为参数)  是
是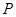 点满足
点满足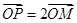 ,
,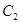 .
. 为极点,
为极点,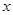 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线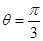 与
与 ,与
,与 ,求
,求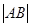 .
.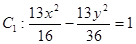 ,点
,点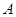 、
、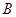 分别为双曲线
分别为双曲线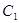 的左、右焦点,动点
的左、右焦点,动点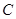 在
在 轴上方.
轴上方.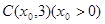 是双曲线的一条渐近线上的点,求以
是双曲线的一条渐近线上的点,求以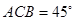 ,求△
,求△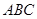 的外接圆的方程;
的外接圆的方程;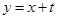 上任取一点
上任取一点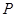 ,从点
,从点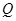 . 问是否存在一个定点
. 问是否存在一个定点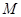 ,恒有
,恒有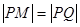 ?请说明理由.
?请说明理由.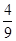 ,求顶点A的轨迹方程.?
,求顶点A的轨迹方程.?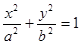
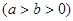 过点
过点 , 且离心率
, 且离心率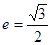 .
.
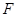 的动直线交椭圆于点
的动直线交椭圆于点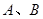 ,设椭圆的左顶点为
,设椭圆的左顶点为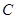 连接
连接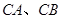 且交动直线
且交动直线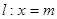 于
于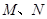 ,若以MN为直径的圆恒过右焦点F,求
,若以MN为直径的圆恒过右焦点F,求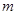 的值.
的值.