题目内容
设函数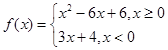 ,若互不相等的实数
,若互不相等的实数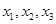 满足
满足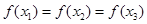 ,则
,则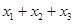 的取值范围是( )
的取值范围是( )
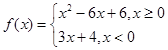 ,若互不相等的实数
,若互不相等的实数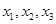 满足
满足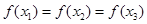 ,则
,则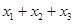 的取值范围是( )
的取值范围是( )A. | B.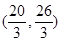 | C. | D. |
D
试题分析:因为实数
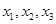 互不相等,设
互不相等,设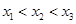 ,根据函数图象知,当
,根据函数图象知,当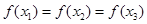 时,
时,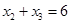 ,而
,而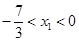 ,所以
,所以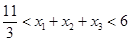 ,选D.
,选D.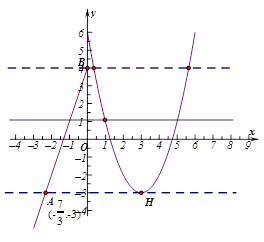

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
题目内容
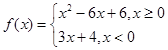 ,若互不相等的实数
,若互不相等的实数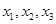 满足
满足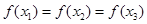 ,则
,则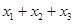 的取值范围是( )
的取值范围是( )A. | B.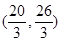 | C. | D. |
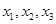 互不相等,设
互不相等,设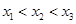 ,根据函数图象知,当
,根据函数图象知,当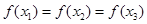 时,
时,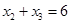 ,而
,而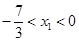 ,所以
,所以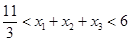 ,选D.
,选D.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案