题目内容
设max{f(x),g(x)}=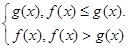 ,若函数n(x)=x2+px+q(p,q∈R)的图象经过不同的两点(
,若函数n(x)=x2+px+q(p,q∈R)的图象经过不同的两点(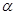 ,0)、(
,0)、(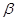 ,0),且存在整数n使得n<
,0),且存在整数n使得n<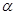 <
<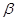 <n+1成立,则( )
<n+1成立,则( )
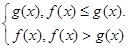 ,若函数n(x)=x2+px+q(p,q∈R)的图象经过不同的两点(
,若函数n(x)=x2+px+q(p,q∈R)的图象经过不同的两点(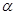 ,0)、(
,0)、(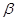 ,0),且存在整数n使得n<
,0),且存在整数n使得n<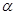 <
<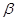 <n+1成立,则( )
<n+1成立,则( )| A.max{n(n),n(n+1)}>1 | B.max{n(n),n(n+1)}<1 |
C.max{n(n),n(n+1)}>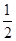 | D.max{n(n),n(n+1)}> 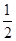 |
B
∵n(x)=x2+px+q的图象经过两点(α,0),(β,0),
∴n(x)=x2+px+q=(x-α)(x-β)
∴n(n)=(n-α)(n-β)=(α-n)(β-n),n(n+1)=(n+1-α)(n+1-β),
令α-n=t1,β-n=t2,由于n<α<β<n+1,则0<t1<1,0<t2<1,且0<t1+t2<2,n(n+1)=(1-t1)(1-t2),
则n(n)= t1t2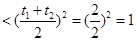 ,即n(n)<1;n(n+1)=(1-t1)(1-t2)
,即n(n)<1;n(n+1)=(1-t1)(1-t2)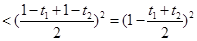 ,
,
∵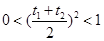 ,∴n(n+1)<1,∴
,∴n(n+1)<1,∴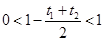 ,
,
∴max{n(n),n(n+1)}<1,故选B.
∴n(x)=x2+px+q=(x-α)(x-β)
∴n(n)=(n-α)(n-β)=(α-n)(β-n),n(n+1)=(n+1-α)(n+1-β),
令α-n=t1,β-n=t2,由于n<α<β<n+1,则0<t1<1,0<t2<1,且0<t1+t2<2,n(n+1)=(1-t1)(1-t2),
则n(n)= t1t2
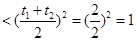 ,即n(n)<1;n(n+1)=(1-t1)(1-t2)
,即n(n)<1;n(n+1)=(1-t1)(1-t2)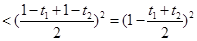 ,
,∵
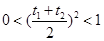 ,∴n(n+1)<1,∴
,∴n(n+1)<1,∴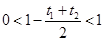 ,
,∴max{n(n),n(n+1)}<1,故选B.

练习册系列答案
相关题目

 ,求
,求 的最大值与最小值;
的最大值与最小值;  的最大值与最小值;
的最大值与最小值;  的图象过点
的图象过点 和
和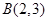 ,则下列各点在函数
,则下列各点在函数



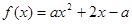 满足
满足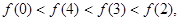 则
则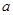 的取值范围为_____
的取值范围为_____ .设
.设 ,
, (max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记
(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记 的最小值为A,
的最小值为A, 的最大值为B,则
的最大值为B,则 ( )
( )


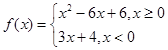 ,若互不相等的实数
,若互不相等的实数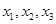 满足
满足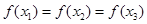 ,则
,则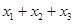 的取值范围是( )
的取值范围是( )