题目内容
在△ABC中,角A、B、C的对边分别为a、b、c,已知向量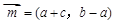 ,
,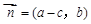 ,
,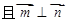 .
.
(1)求角C的大小; (2)若 ,求角A的值.
,求角A的值.
(1)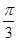 ;(2)
;(2)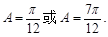
解析试题分析:解题思路:(1)利用平面向量的垂直的判定得出三角形的三边的关系式,在利用余弦定理求角;(2)利用三角形的三角关系进行消元,使其变为关于角A的式子,再恒等变形求角的正弦值,结合角的范围求角.规律总结:对于以平面向量为载体考查三角函数问题,要正确利用平面向量知识化为三角函数关系式,再利用三角函数的有关公式进行变形.
注意点:利用三角函数值求角时,一定要结合角所在的范围求角.
试题解析:(1) 由
整理得
即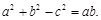
又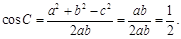
又因为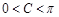 ,
,
所以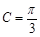
(2) 因为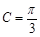 ,所以
,所以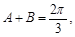
故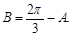
由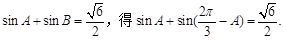
即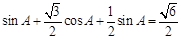 ,
,
所以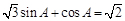 .
.
即 .
.
因为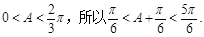
故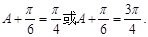
所以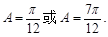
考点:1.平面向量垂直的判定;2余弦定理;3.三角恒等变换.

练习册系列答案
相关题目
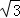 .
. ,
,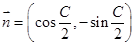 ,且
,且 的夹角是
的夹角是
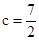 ,三角形ABC的面积
,三角形ABC的面积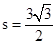 ,求a+b.
,求a+b.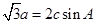 .
.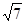 ,且△ABC的面积为
,且△ABC的面积为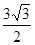
 ,求a+b的值.
,求a+b的值.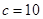 , 又知
, 又知 ,求边
,求边 、
、 的长.
的长.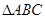 中,内角
中,内角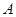 ,
, ,
,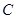 所对的边分别为
所对的边分别为 ,
,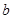 ,
,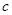 ,已知
,已知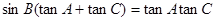 .
.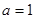 ,
,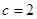 ,求
,求 .
.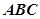 中,角
中,角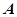 、
、 、
、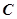 的对边分别为
的对边分别为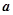 、
、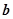 、
、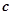 ,且
,且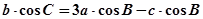 .
.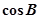 ;
;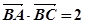 ,且
,且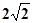 ,求
,求 两地连线上的定点
两地连线上的定点 处建造广告牌
处建造广告牌 ,其中
,其中 为顶端,
为顶端, 长35米,
长35米, 长80米,设
长80米,设 和
和 看
看 .
.
 ,问
,问 求
求 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且
,且 ,
, ,
, .
. 与边
与边 在
在 方向上的投影.
方向上的投影.