题目内容
某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如下：
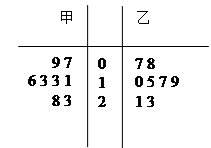
（1）比较这两名队员在比赛中得分的均值和方差的大小；（4分）
（2）以上述数据统计甲、乙两名队员得分超过15分的频率作为概率，假设甲、乙两名队员在同一场比赛中得分多少互不影响，预测在本赛季剩余的2场比赛中甲、乙两名队员得分均超过15分的次数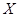
的分布列和均值．（8分）
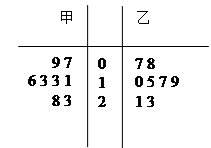
（1）比较这两名队员在比赛中得分的均值和方差的大小；（4分）
（2）以上述数据统计甲、乙两名队员得分超过15分的频率作为概率，假设甲、乙两名队员在同一场比赛中得分多少互不影响，预测在本赛季剩余的2场比赛中甲、乙两名队员得分均超过15分的次数
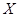的分布列和均值．（8分）（Ⅰ）甲、乙两名队员的得分均值相等；甲的方差较大（乙的方差较小）．
（Ⅱ）X的分布列为
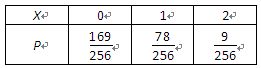
X的均值E(X)＝2×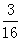
＝
．
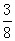（Ⅱ）X的分布列为
X的均值E(X)＝2×
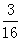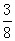＝． （1）根据平均数和方差公式计算即可；（2）先根据古典概型求出概率，然后利用二项分布知识求出随机变量的分布列及期望
（Ⅰ）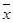
甲＝
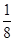(7＋9＋11＋13＋13＋16＋23＋28)＝15，
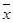乙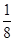＝ (7＋8＋10＋15＋17＋19＋21＋23)＝15，
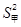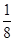＝ [(－8)2＋(－6)2＋(－4)2＋(－2)2＋(－2)2＋12＋82＋132]＝44.75，
s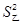
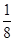＝ [(－8)2＋(－7)2＋(－5)2＋02＋22＋42＋62＋82]＝32.25．
甲、乙两名队员的得分均值相等；甲的方差较大（乙的方差较小）．…4分
（Ⅱ）根据统计结果，在一场比赛中，甲、乙得分超过15分的概率分别为p1＝，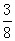
p2＝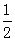
，两人得分均超过15分的概率分别为p1p2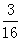＝，┈┈5分
依题意，X～B(2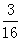，)，P(X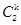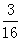＝k)＝
()k(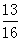
)2－k，k＝0，1，2， …7分
X的分布列为
…10分
X的均值E(X)＝2×＝．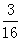
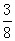（Ⅰ）
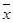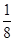甲＝(7＋9＋11＋13＋13＋16＋23＋28)＝15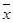，乙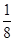＝ (7＋8＋10＋15＋17＋19＋21＋23)＝15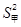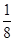，＝ [(－8)2＋(－6)2＋(－4)2＋(－2)2＋(－2)2＋12＋82＋132]＝44.75，s
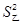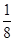＝ [(－8)2＋(－7)2＋(－5)2＋02＋22＋42＋62＋82]＝32.25．甲、乙两名队员的得分均值相等；甲的方差较大（乙的方差较小）．…4分
（Ⅱ）根据统计结果，在一场比赛中，甲、乙得分超过15分的概率分别为p1＝
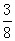，p2＝
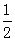，两人得分均超过15分的概率分别为p1p2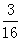＝，┈┈5分依题意，X～B(2，
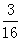)，P(X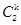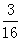＝k)＝()k(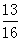)2－k，k＝0，1，2， …7分X的分布列为
…10分X的均值E(X)＝2×
＝．
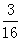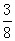练习册系列答案
相关题目
，则E
，乙获胜的概率为
，假定各次比赛相互独立，比赛经ξ次结束，求：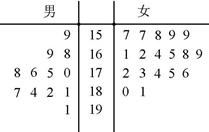
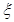表示所选代表中女“运动健将”的人数，试写出
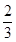，被乙小组攻克的概率为
，
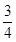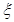为攻关期满时获奖的攻关小组数，求
；
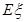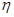为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方，记“函数
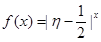在定义域内单调递增”为事件C，求事件C发生的概率；
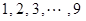班参加高考体检，
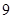个班中，任选
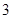个班先参加视力检查． （I）求这
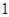个班班级序号是偶数的概率；
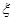为这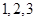
班，则有两组相邻的，
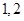班和
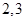班，此时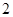
）．求随机变量
．
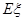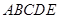五个不同区域，要求同一区域上用同一种颜色的鲜花，相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择．
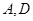区域同时用红色鲜花时，求布置花圃的不同方法的种数；
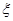为花圃中用红色鲜花布置的区域的个数，求随机变量