Question

【题目】已知随机变量 的取值为不大于 的非负整数值，它的分布列为：

	0	1	2		n

其中 （ ）满足： ，且 ．
定义由 生成的函数 ，令 ．
（I）若由 生成的函数 ，求 的值；
（II）求证：随机变量 的数学期望 ， 的方差 ；
（ ）
（Ⅲ）现投掷一枚骰子两次，随机变量 表示两次掷出的点数之和，此时由 生成的函数记为 ，求 的值．

Answer 1

【答案】解：（I） ．

（II）由于 ，

，

所以 ．

由 的方差定义可知

由于 ，所以有

，这样

，所以有

．

（III）由题意可知 的取值为2,3,4,5,6,7,8,9,10,11,12

则 的分布列为

	2	3	4	5	6	7	8	9	10	11	12

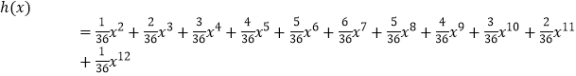则

【解析】(1)由题意可求出其值。(2)结合题意根据数学期望值得公式即可求出结果。(2)根据题意可知 ξ 的取值由题意可求出各个取值的概率列表求出即可。
【考点精析】利用离散型随机变量及其分布列对题目进行判断即可得到答案，需要熟知在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列．