题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,若曲线
时,若曲线![]() 在直线
在直线![]() 的上方,求实数
的上方,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据题意,求出函数的导数,由导数的几何意义可得切线的斜率,求出切点的坐标,由直线的点斜式方程分析可得答案;(2)根据题意,原问题可以转化为![]() 恒成立,设
恒成立,设![]() ,求出
,求出![]() 的导数,由函数的导数与函数单调性的关系分析可得其最大值,分析可得答案.
的导数,由函数的导数与函数单调性的关系分析可得其最大值,分析可得答案.
(1)当![]() 时,
时,![]() ,其导数
,其导数![]() ,
,![]() .
.
又因为![]() ,
,
所以曲线y=f(x)在点(0,f(0))处的切线方程为![]() ;
;
(2)根据题意,当![]() 时,
时,
“曲线y=f(x)在直线![]() 的上方”等价于“
的上方”等价于“![]() 恒成立”,
恒成立”,
又由x>0,则![]()
![]()
![]() ,
,
则原问题等价于![]() 恒成立;
恒成立;
设![]() ,则
,则![]() ,
,
又由![]() ,则
,则![]() ,则函数
,则函数![]() 在区间
在区间![]() 上递减,
上递减,
又由![]() ,则有
,则有![]() ,
,
若![]() 恒成立,必有
恒成立,必有![]() ,
,
即![]() 的取值范围为
的取值范围为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
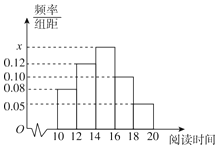
小学生10分钟应用题系列答案【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了各级城市的大街小巷,为了解我市的市民对共享单车的满意度,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了50人进行分析.若得分低于60分,说明不满意,若得分不低于60分,说明满意,调查满意度得分情况结果用茎叶图表示如图1.
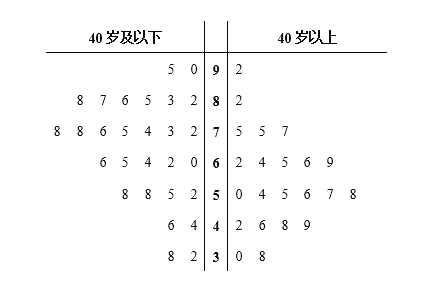
(Ⅰ)根据茎叶图找出40岁以上网友中满意度得分的众数和中位数;
(Ⅱ)根据茎叶图完成下面列联表,并根据以上数据,判断是否有![]() 的把握认为满意度与年龄有关;
的把握认为满意度与年龄有关;
满意 | 不满意 | 合计 | |
40岁以下 | |||
40岁以上 | |||
合计 |
(Ⅲ)先采用分层抽样的方法从40岁及以下的网友中选取7人,再从这7人中随机选出2人,将频率视为概率,求选出的2人中至少有1人是不满意的概率.
参考格式: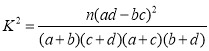 ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某幼儿园雏鹰班的生活老师统计2018年上半年每个月的20日的昼夜温差![]() ,
,![]() 和患感冒的小朋友人数(
和患感冒的小朋友人数(![]() /人)的数据如下:
/人)的数据如下:
温差 |
|
|
|
|
|
|
患感冒人数 | 8 | 11 | 14 | 20 | 23 | 26 |
其中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)请用相关系数加以说明是否可用线性回归模型拟合![]() 与
与的关系;
(Ⅱ)建立![]() 关于
关于![]() 的回归方程(精确到
的回归方程(精确到![]() ),预测当昼夜温差升高
),预测当昼夜温差升高![]() 时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
参考数据:![]() .参考公式:相关系数:
.参考公式:相关系数: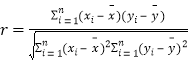 ,回归直线方程是
,回归直线方程是![]() ,
,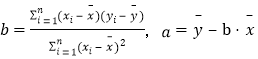 ,
,