题目内容
【题目】对给定的d∈N*,记由数列构成的集合![]() .
.
(1)若数列{an}∈Ω(2),写出a3的所有可能取值;
(2)对于集合Ω(d),若d≥2.求证:存在整数k,使得对Ω(d)中的任意数列{an},整数k不是数列{an}中的项;
(3)已知数列{an},{bn}∈Ω(d),记{an},{bn}的前n项和分别为An,Bn.若|an+1|≤|bn+1|,求证:An≤Bn.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)推导出![]() ,
,![]() ,
,![]() ,
,![]() ,由此能求出
,由此能求出![]() 的所有可能取值;(2)先应用数学归纳法证明数列
的所有可能取值;(2)先应用数学归纳法证明数列![]() ,则
,则![]() 具有
具有![]() ,(
,(![]() )的形式,由此能证明取整数
)的形式,由此能证明取整数![]() ,则整数
,则整数![]() 均不是数列
均不是数列![]() 中的项;(3)由
中的项;(3)由![]() ,得:
,得:![]() ,从而
,从而![]() ,由此利用累加法得
,由此利用累加法得![]() ,从而
,从而![]() ,同理
,同理![]() ,由此能证明
,由此能证明![]() .
.
(1)由于数列{an}∈Ω(2),即d=2,a1=1.
由已知有|a2|=|a1+d|=|1+2|=3,所以a2=±3,
|a3|=|a2+d|=|a2+2|,
将a2=±3代入得a3的所有可能取值为-5,-1,1,5.
证明:(2)先应用数学归纳法证明数列:
若{an}∈Ω(d),则an具有md±1,(m∈Z)的形式.
①当n=1时,a1=0d+1,因此n=1时结论成立.
②假设当n=k(k∈N*)时结论成立,即存在整数m0,使得ak=m0d0±1成立.
当n=k+1时,|an+1|=|m0d0±1+d0|=|(m0+1)d0±1|,
ak+1=(m0+1)d±1,或ak+1=-(m0+1)±1,
所以当n=k+1时结论也成立.
由①②可知,若数列{an}∈Ω(d)对任意n∈N*,an具有md±1(m∈Z)的形式.
由于an具有md±1(m∈Z)的形式,以及d≥2,可得an不是d的整数倍.
故取整数k=d,则整数k均不是数列{an}中的项
(3)由|an+1|=|an+d|,可得:![]() =
=![]() ,
,
所以有![]() =
=![]() +2and+d2,
+2and+d2,
![]() =
=![]() +2an-1d+d2,
+2an-1d+d2,
![]() ,
,
…
![]() =
=![]() ,
,
以上各式相加可得![]() ,
,
即An=![]() -
-![]() ,同理Bn=
,同理Bn=![]() -
-![]() ,
,
当![]() 时,有
时,有![]() ,
,
∵d∈N*,∴![]() ≤
≤![]() ,
,
∴![]() ≤
≤![]() -
-![]() ,
,
∴![]()

【题目】2020年寒假是特殊的寒假,因为抗击疫情全体学生只能在家进行网上在线学习,为了研究学生在网上学习的情况,某学校在网上随机抽取120名学生对线上教育进行调查,其中男生与女生的人数之比为11∶13,其中男生30人对于线上教育满意,女生中有15名表示对线上教育不满意.
(1)完成![]() 列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
满意 | 不满意 | 总计 | |
男生 | 30 | ||
女生 | 15 | ||
合计 | 120 |
(2)从被调查的对线上教育满意的学生中,利用分层抽样抽取8名学生,再在8名学生中抽取3名学生,作线上学习的经验介绍,其中抽取男生的个数为![]() ,求出
,求出![]() 的分布列及期望值.
的分布列及期望值.
参考公式:附: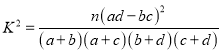
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 0.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10828 |
【题目】2018年,南昌市召开了全球VR产业大会,为了增强对青少年VR知识的普及,某中学举行了一次普及VR知识讲座,并从参加讲座的男生中随机抽取了50人,女生中随机抽取了70人参加VR知识测试,成绩分成优秀和非优秀两类,统计两类成绩人数得到如下的列联表:
优秀 | 非优秀 | 总计 | |
男生 | a | 35 | 50 |
女生 | 30 | d | 70 |
总计 | 45 | 75 | 120 |
(1)确定a,d的值;
(2)试判断能否有90%的把握认为VR知识的测试成绩优秀与否与性别有关;
(3)为了宣传普及VR知识,从该校测试成绩获得优秀的同学中按性别采用分层抽样的方法,随机选出6名组成宣传普及小组.现从这6人中随机抽取2名到校外宣传,求“到校外宣传的2名同学中至少有1名是男生”的概率.
附:![]()
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |