题目内容

【题目】如图，某种螺帽是由一个半径为2的半球体挖去一个正三棱锥构成的几何体，该正三棱锥的底面三角形内接于半球底面大圆，顶点在半球面上，则被挖去的正三棱锥体积为_______．

【答案】

【解析】

设BC的中点为D，连结AD，过点P作PO平面ABC，角AD于点O，则A0=PO=R=2，AD=3，AB=BC=，由此能求出挖去的正三棱锥的体积，得到答案.

由题意，某中螺帽是由一个半径为R=2的半球体挖去一个正三棱锥P-ABC构成的几何体，

该正三棱锥P-ABC的底面三角形ABC内接于半球底面的大圆，顶点P在半球面上，

设BC的中点为D，连结AD，过点P作PO平面ABC，交AD于点O，

则AO=PO=R=2，AD=3，AB=BC=，

所以，

所以挖去的正三棱锥的体积为.

练习册系列答案
相关题目

【题目】已知函数．

（1）若函数在区间上是增函数，求实数的取值范围；

（2）若是函数的极值点，求函数在上的最大值；

（3）在(2)的条件下，是否存在实数，使得函数的图象与函数的图象恰有个交点？若存在，请求出的取值范围；若不存在，请说明理由．

【题目】已知函数．

（1）当时，求曲线在点处的切线方程；

（2）当时，若曲线在直线的上方，求实数的取值范围．

【题目】如图，在平面直角坐标系xOy中，已知焦点在x轴上，离心率为的椭圆E的左顶点为A，点A到右准线的距离为6．

（1）求椭圆E的标准方程；

（2）过点A且斜率为的直线与椭圆E交于点B，过点B与右焦点F的直线交椭圆E于M点，求M点的坐标．

【题目】已知函数，其中．

（1）函数在处的切线与直线垂直，求实数a的值；

（2）若函数在定义域上有两个极值点，，且．

①求实数a的取值范围；

②求证：．

【题目】2018年，南昌市召开了全球VR产业大会，为了增强对青少年VR知识的普及，某中学举行了一次普及VR知识讲座，并从参加讲座的男生中随机抽取了50人，女生中随机抽取了70人参加VR知识测试，成绩分成优秀和非优秀两类，统计两类成绩人数得到如下的列联表：

优秀

非优秀

总计

男生

a

35

50

女生

30

d

70

总计

45

75

120

（1）确定a,d的值；

（2）试判断能否有90%的把握认为VR知识的测试成绩优秀与否与性别有关；

（3）为了宣传普及VR知识，从该校测试成绩获得优秀的同学中按性别采用分层抽样的方法，随机选出6名组成宣传普及小组．现从这6人中随机抽取2名到校外宣传，求“到校外宣传的2名同学中至少有1名是男生”的概率.

附：

P(K2≥k0)

0.25

0.15

0.10

0.05

0.025

0.010

k0

1.323

2.072

2.706

3.841

5.024

6.635

【题目】（2017高考新课标Ⅲ，理19）如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．

（1）证明：平面ACD⊥平面ABC；

（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D–AE–C的余弦值.

【题目】某地最近十年粮食需求量逐年上升，下表是部分统计数据：

年份

2006

2008

2010

2012

2014

需求量/万吨

236

246

257

276

286

（1）利用所给数据求年需求量与年份之间的线性回归方程；

（2）利用（1）中所求出的线性回归方程预测该地2018年的粮食需求量.

参考公式：，.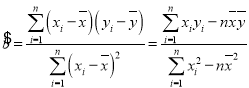

【题目】随着工业化以及城市车辆的增加，城市的空气污染越来越严重，空气质量指数一直居高不下，对人体的呼吸系统造成了严重的影响.现调查了某市名居民的工作场所和呼吸系统健康，得到列联表如下：

室外工作

室内工作

合计

有呼吸系统疾病

无呼吸系统疾病

合计

（Ⅰ）补全列联表；

（Ⅱ）你是否有的把握认为感染呼吸系统疾病与工作场所有关；

（Ⅲ）现采用分层抽样从室内工作的居民中抽取一个容量为的样本，将该样本看成一个总体，从中随机的抽取两人，求两人都有呼吸系统疾病的概率.

临界值表：

0.100

0.050

0.025

0.010

0.001

2.706

3.841

5.024

6.635

10.828

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网