在△ABC中.a.b.c分别为角A.B.C所对的边.若a=4.A=30°.则$\frac{b+c}{sinB+sinC}$的值为8．题目和参考答案——青夏教育精英家教网—

题目内容

17．在△ABC中，a，b，c分别为角A，B，C所对的边，若a=4，A=30°，则$\frac{b+c}{sinB+sinC}$的值为8．

分析由正弦定理化简可得$\frac{b+c}{sinB+sinC}$=$\frac{2RsinB+2RsinC}{sinB+sinC}$=2R=$\frac{a}{sinA}$，即可得解．

解答解：由正弦定理得：$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$，
∴b=2RsinB，c=2RsinC，
∴$\frac{b+c}{sinB+sinC}$=$\frac{2RsinB+2RsinC}{sinB+sinC}$=2R=$\frac{a}{sinA}$=$\frac{4}{sin30°}$=8．
故答案为：8；

点评本题主要考查正弦定理的应用，属于基础题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

8．对于函数y=f（x），当x∈（0，+∞）时，总有f（x）＜xf′（x），若m＞n＞0，下列不等式中能恒成立的是（　　）

A．

$\frac{f（m）}{m}＜\frac{f（n）}{n}$

B．

$\frac{f（m）}{m}＞\frac{f（n）}{n}$

C．

$\frac{f（m）}{n}＞\frac{3f（n）}{m}$

D．

$\frac{f（m）}{n}＜\frac{f（n）}{m}$

5．已知|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=3，$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°．
（Ⅰ）求（3$\overrightarrow{a}-\overrightarrow{b}$）$•（\overrightarrow{a}+2\overrightarrow{b}）$的值；
（Ⅱ）求|$\overrightarrow{a}+\overrightarrow{b}$|的值．

12．（2-x）¹⁰=a₀+a₁x+a₂x²+…+a₁₀x¹⁰．则a₁+a₂+a₃+…+a₁₀=（　　）

2．从装有5个红球和5个黑球的口袋中任取3个球，则至少有一个红球的概率是（　　）

9．在四边形ABCD中，若$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$，且$|{\overrightarrow{AB}}|=|{\overrightarrow{AD}}|$，则（　　）

	A．	ABCD是矩形		B．	ABCD是菱形
	C．	ABCD是正方形		D．	ABCD是平行四边形

6．

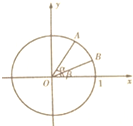如图，在平面直角坐标系xOy中，以Ox轴为始边作两个锐角α，β，它们的终边分别与单位圆相交于A、B两点，已知A、B的横坐标分别为$\frac{5}{13}，\frac{3}{5}$，则tan（α+β）的值为-$\frac{56}{33}$．

7．

一个多面体的三视图如图所示，其中正视图是正方形，侧视图是等腰三角形，则该几何体的表面积是（　　）

试题分类