题目内容
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (t为参数),直线
(t为参数),直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).设
为参数).设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时,
变化时,![]() 的轨迹为曲线
的轨迹为曲线![]()
(1)写出![]() 的普通方程;
的普通方程;
(2)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,设
轴正半轴为极轴建立极坐标系,设![]() ,
,![]() 为
为![]() 与
与![]() 的交点,求
的交点,求![]() 的极径.
的极径.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)分别消掉参数t与m可得直线l1与直线l2的普通方程为y=k(x-2)①与x=-2+ky②;联立①②,消去k可得C的普通方程为x2-y2=4;
(2)将l的极坐标方程与曲线C的极坐标方程联立,可得关于θ的方程,解得tanθ,即可求得l与C的交点M的极径为ρ.
(1)消去参数t,得l1的普通方程l1:y=k(x-2);
消去参数m,得l2的普通方程l2:y=![]() (x+2). 设P(x,y),由题设得
(x+2). 设P(x,y),由题设得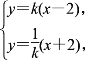
消去k,得x2-y2=4(y≠0),所以C的普通方程为x2-y2=4(y≠0).
(2)C的极坐标方程为ρ2(cos2θ-sin2θ)=4(0<θ<2π,θ≠π),
联立![]() 得cos θ-sin θ=2(cos θ+sin θ).
得cos θ-sin θ=2(cos θ+sin θ).
故tan θ=-![]() ,从而cos2θ=
,从而cos2θ=![]() ,sin2θ=
,sin2θ=![]() .
.
代入ρ2(cos2θ-sin2θ)=4,得ρ2=5,所以l与C的交点M的极径为![]() .
.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
试销单价x(元) | 4 | 5 | 6 | 7 | 8 |
产品销量y(件) | q | 85 | 82 | 80 | 75 |
已知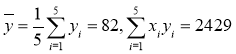
(1)求出q的值;
(2)已知变量![]() 具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程
具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程![]() ;
;
(3)假设试销单价为10元,试估计该产品的销量.