题目内容
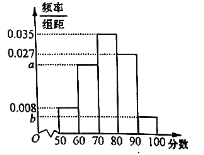
【题目】近年来,石家庄经济快速发展,跻身新三线城市行列,备受全国瞩目.无论是市内的井字形快速交通网,还是辐射全国的米字形高铁路网,石家庄的交通优势在同级别的城市内无能出其右.为了调查石家庄市民对出行的满意程度,研究人员随机抽取了1000名市民进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)求被调查的市民的满意程度的平均数,中位数(保留小数点后两位),众数;
(3)若按照分层抽样从![]() ,
,![]() 中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在
中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在![]() 的概率.
的概率.
【答案】(1)![]() ,
,![]() ;(2)平均数约为
;(2)平均数约为![]() ,中位数约为
,中位数约为![]() ,众数约为75;(3)
,众数约为75;(3)![]() .
.
【解析】
(1)根据题目频率分布直方图频率之和为1,已知其中![]() ,可得答案;
,可得答案;
(2)利用矩形的面积等于频率为0.5可估算中位数所在的区间,利用估算中位数定义,矩形最高组估算纵数可得答案;
(3)利用古典概型的概率计算公式求解即可.
解:研究人员随机抽取了1000名市民进行调查,并将满意程度以分数的形式统计成如图的频率分布直方图,其中![]() ,
,
(1)![]() ,其中
,其中![]() ,解得:
,解得:![]() ,
,![]() ;
;
(2)随机抽取了1000名市民进行调查,则估计被调查的市民的满意程度的
平均数:![]() ,
,
由题中位数在70到80区间组,![]() ,
,![]() ,
,
中位数:![]() ,
,
众数:75,
故平均数约为![]() ,中位数约为
,中位数约为![]() ,众数约为75;
,众数约为75;
(3)若按照分层抽样从![]() ,
,![]() ,
,![]() ,
,![]() 中随机抽取8人,
中随机抽取8人,
则![]() ,
,![]() 共80人抽2人,
共80人抽2人,
![]() ,
,![]() 共240人抽6人,
共240人抽6人,
再从这8人中随机抽取2人,则共有![]() 种不同的结果,
种不同的结果,
其中至少有1人的分数在![]() ,
,![]() 共
共![]() 种不同的结果,
种不同的结果,
所以至少有1人的分数在![]() ,
,![]() 的概率为:
的概率为:![]() .
.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目