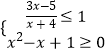题目内容
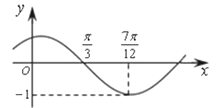
【题目】已知函数
．
（Ⅰ）若函数
在
处的切线平行于直线
，求实数a的值；
（Ⅱ）判断函数
在区间
上零点的个数；
（Ⅲ）在（Ⅰ）的条件下，若在
上存在一点
，使得
成立，求实数
的取值范围．
【答案】（1）
（2）
时， 
在
无零点； 
时， 
在
恰有一个零点； 
时， 
在
有两个零点（3）
或
【解析】试题分析：（1）利用导数的几何意义，得
， 
；（2）函数的零点个数等价于两个函数的交点的个数，即
与
的交点个数；（3）不等式能成立问题转化为函数的最值问题.
试题解析：
（Ⅰ）
,函数
在
处的切线平行于直线
.
.
（Ⅱ）令
， 
得
记
， 
由此可知
在
上递减，在
上递增，
且
时
故
时， 
在
无零点
时， 
在
恰有一个零点
时， 
在
有两个零点
（Ⅲ）在
上存在一点
,使得
成立等价于函数
在
上的最小值小于零.
,
①当
时,即
时, 
上单调递减,所以
的最小值为
,由
可得
,
；
②当
时,即
时, 
在
上单调递增,所以
的最小值为
,由
可得
；
③当
时,即
时,可得
的最小值为
此时, 
不成立.
综上所述:可得所求
的范围是
或
名校课堂系列答案
【题目】随着移动互联网的快速发展，基于互联网的共享单车应运而生．某市场研究人员为了了解共享单车运营公司M的经营状况，对该公司最近六个月内的市场占有率进行了统计，并绘制了相应的折线图．
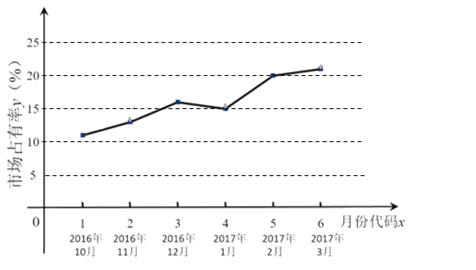
（Ⅰ）由折线图可以看出，可用线性回归模型拟合月度市场占有率y与月份代码x之间的关系．求y关于x的线性回归方程，并预测M公司2017年4月份（即x=7时）的市场占有率；
（Ⅱ）为进一步扩大市场，公司拟再采购一批单车．现有采购成本分别为1000元/辆和1200元/辆的A、B两款车型可供选择，按规定每辆单车最多使用4年，但由于多种原因（如骑行频率等）会导致车辆报废年限各不相同．考虑到公司运营的经济效益，该公司决定先对两款车型的单车各100辆进行科学模拟测试，得到两款单车使用寿命频数表如下：
车型 | 1年 | 2年 | 3年 | 4年 | 总计 |
A | 20 | 35 | 35 | 10 | 100 |
B | 10 | 30 | 40 | 20 | 100 |
经测算，平均每辆单车每年可以带来收入500元．不考虑除采购成本之外的其他成本，假设每辆单车的使用寿命都是整数年，且以频率作为每辆单车使用寿命的概率．如果你是M公司的负责人，以每辆单车产生利润的期望值为决策依据，你会选择采购哪款车型？
参考数据： 
（参考公式：回归直线方程为
，其中
）
