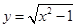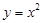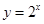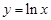题目内容
若关于 的方程
的方程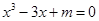 在
在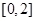 上有根,则实数
上有根,则实数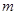 的取值范围是 ( )
的取值范围是 ( )
A.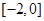 | B.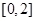 | C.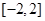 | D. |
C
解析试题分析:根据题意,由于关于 的方程
的方程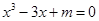 在
在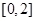 上有根,则可知
上有根,则可知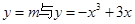 在给定区间上有交点,则利用
在给定区间上有交点,则利用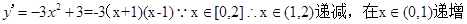 ,只要满足函数的极大值大于等于m即可,最小值小于等于m,而极大值即为x=1时,得到为2,最小值为-2,故可知实数
,只要满足函数的极大值大于等于m即可,最小值小于等于m,而极大值即为x=1时,得到为2,最小值为-2,故可知实数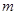 的取值范围
的取值范围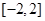 ,选C.
,选C.
考点:函数与方程
点评:解决含有参数的方程根 的问题,转化为两个图像与图像的交点问题来解决,属于基础题。

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
已知定义在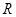 上的偶函数
上的偶函数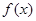 满足
满足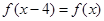 ,且在区间[0,2]上
,且在区间[0,2]上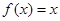 ,若关于
,若关于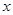 的方程
的方程 有三个不同的根,则
有三个不同的根,则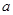 的范围为
的范围为
A.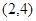 | B.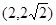 | C.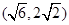 | D.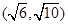 |
已知函数 的定义域为
的定义域为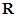 ,满足
,满足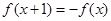 ,且当
,且当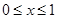 时,
时,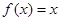 ,
,
则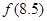 等于( )
等于( )
A.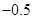 | B.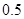 | C.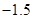 | D.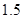 |
设f(x)是定义在R的偶函数,对任意xÎR,都有f(x-2)=f(x+2),且当xÎ[-2, 0]时, f(x)=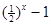 .若在区间(-2,6]内关于x的方程
.若在区间(-2,6]内关于x的方程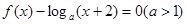 恰有3个不同的实数根,则实数a的取值范围是( )
恰有3个不同的实数根,则实数a的取值范围是( )
| A.(1, 2) | B.(2,+¥) | C.(1,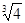 ) ) | D.(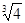 , 2) , 2) |
如图是导函数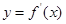 的图象,则下列命题错误的是( )
的图象,则下列命题错误的是( )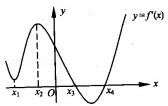
A.导函数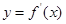 在 在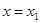 处有极小值 处有极小值 |
B.导函数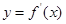 在 在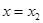 处有极大值 处有极大值 |
C.函数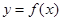 在 在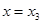 处有极小值 处有极小值 |
D.函数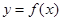 在 在 处有极小值 处有极小值 |
下列函数中,在其定义域内既是奇函数又是减函数的是( )
| A.y=-x3,x∈R | B.y=sinx,x∈R |
| C.y=x,x∈R | D.y=(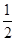 )x,x∈R )x,x∈R |
函数y=x+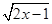 ( )
( )
A.有最小值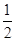 ,无最大值 ,无最大值 |
B.有最大值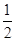 ,无最小值 ,无最小值 |
C.有最小值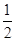 ,最大值2 ,最大值2 |
| D.无最大值,也无最小值 |
下列函数中,是奇函数且在区间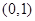 内单调递减的函数是( )
内单调递减的函数是( )
A.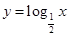 | B.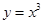 | C.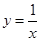 | D.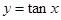 |
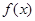 ,如果存在锐角
,如果存在锐角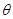 使得
使得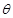 ,所得曲线仍是一函数,则称函数
,所得曲线仍是一函数,则称函数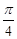 的旋转性的是( )
的旋转性的是( )