题目内容
已知关于x的函数y=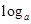 (2-ax)在[0,1]上是减函数,则a的取值范围是
(2-ax)在[0,1]上是减函数,则a的取值范围是
| A.(0,1) | B.(1,2) | C.(0,2) | D.[2,+∞)] |
B
解析试题分析:因为关于x的函数y=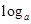 (2-ax)在[0,1]上是减函数,而a>0,u=2-ax是减函数,所以y=
(2-ax)在[0,1]上是减函数,而a>0,u=2-ax是减函数,所以y=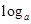 u是增函数,因此,a>1且2-a×1>0,1<a<2,故选B。
u是增函数,因此,a>1且2-a×1>0,1<a<2,故选B。
考点:本题主要考查复合对数函数的单调性。
点评:易错题,复合函数的单调性判定方法是:内外层函数的单调性“同增异减”。该题要注意对数的真数大于零。

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
函数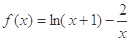 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A.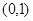 | B.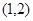 | C.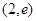 | D.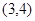 |
已知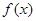 是定义在R上的偶函数,在区间
是定义在R上的偶函数,在区间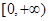 上为增函数,且
上为增函数,且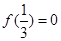 ,则不等式
,则不等式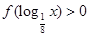 的解集为( )
的解集为( )
A.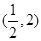 | B.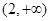 |
C.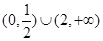 | D.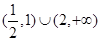 |
下列函数中x=0是极值点的函数是( )
A.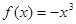 | B.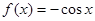 | C.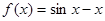 | D.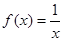 |
使得函数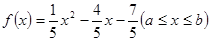 的值域为
的值域为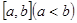 的实数对
的实数对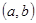
有( )对
| A.1 | B.2 | C.3 | D.无数 |
函数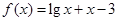 的零点所在区间为
的零点所在区间为
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,+∞) |
已知定义在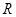 上的偶函数
上的偶函数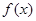 满足
满足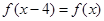 ,且在区间[0,2]上
,且在区间[0,2]上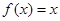 ,若关于
,若关于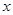 的方程
的方程 有三个不同的根,则
有三个不同的根,则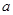 的范围为
的范围为
A.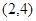 | B.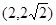 | C.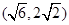 | D.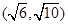 |
下列函数中,在其定义域内既是奇函数又是减函数的是( )
| A.y=-x3,x∈R | B.y=sinx,x∈R |
| C.y=x,x∈R | D.y=(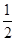 )x,x∈R )x,x∈R |
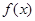 ,如果存在锐角
,如果存在锐角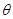 使得
使得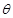 ,所得曲线仍是一函数,则称函数
,所得曲线仍是一函数,则称函数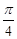 的旋转性的是( )
的旋转性的是( )