题目内容
在三棱锥P-ABC内,已知PA=PC=AC=,AB=BC=1,面PAC⊥面ABC,E是BC的中点.

(1)求直线PE与AC所成角的余弦值;
(2)求直线PB与平面ABC所成的角的正弦值;
(3)求点C到平 面PAB的距
面PAB的距 离.
离.

(1)求直线PE与AC所成角的余弦值;
(2)求直线PB与平面ABC所成的角的正弦值;
(3)求点C到平
 面PAB的距
面PAB的距 离.
离.解:(1)分别取AB,AC的中点F,H,连结PH,HF,HE,EF
由于E、F分别是BC、AB的中点,故EF是△ABC的中位线,则有EF//AC,
故∠PEF是异面直线PE与AC所成的角或补角
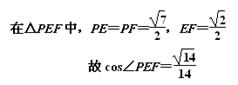
(2)由于PA=PC,H是AC的中点,
有PH⊥AC
又由面PAC⊥面ABC
面PAC∩面ABC=AC
有PH⊥面ABC
故 ∠PBH是直线PB与平面ABC所成的角
∠PBH是直线PB与平面ABC所成的角
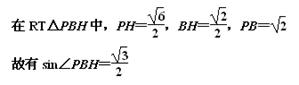
(3)VP-ABC=VC-PAB
可解得: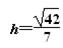
由于E、F分别是BC、AB的中点,故EF是△ABC的中位线,则有EF//AC,
故∠PEF是异面直线PE与AC所成的角或补角
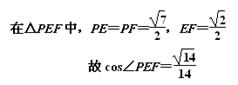
(2)由于PA=PC,H是AC的中点,
有PH⊥AC
又由面PAC⊥面ABC
面PAC∩面ABC=AC
有PH⊥面ABC
故
 ∠PBH是直线PB与平面ABC所成的角
∠PBH是直线PB与平面ABC所成的角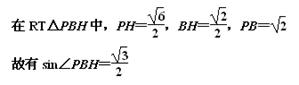
(3)VP-ABC=VC-PAB
可解得:
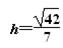
略

练习册系列答案
相关题目
 ,
, ,
,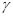 两两互相垂直,点
两两互相垂直,点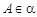 ,点
,点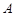 到
到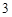 ,点
,点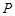 是
是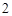 倍,则点
倍,则点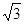
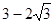
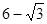
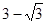
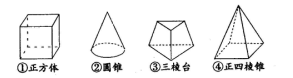
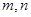 为直线,
为直线,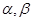 为平面,给出下列命题:
为平面,给出下列命题: ②
②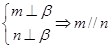 ③
③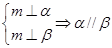 ④
④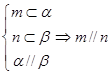
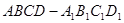 的侧面
的侧面 内有一动点
内有一动点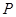 到直线
到直线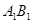 与直线
与直线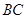 的距离相等,则动点
的距离相等,则动点
 中,平面
中,平面 ∥平面
∥平面 ,
,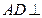 平面
平面 ,
,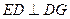 ,
,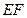 ∥
∥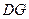 ,且
,且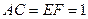 ,
,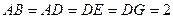 .
.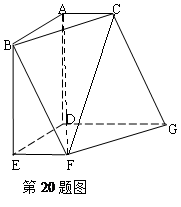
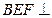 平面
平面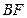 ∥平面
∥平面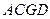 ;
;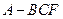 的体积.
的体积.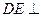 平面ABCD,
平面ABCD,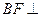 平面ABCD,且FB=2DE=2。
平面ABCD,且FB=2DE=2。
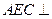 平面AFC。
平面AFC。 分米,半径是10分米的扇形胶片制作一个圆锥体模型,这个圆锥体的体积等于_ __立方分米.
分米,半径是10分米的扇形胶片制作一个圆锥体模型,这个圆锥体的体积等于_ __立方分米.