题目内容
若椭圆的短轴为
,一个焦点为
,且
为等边三角形的椭圆的离心率是( )
A． | B． | C． | D． |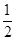
B
解析试题分析：因为椭圆的短轴长为
，
，所以
考点：本小题主要考查椭圆中基本量的计算和离心率的求法，考查学生的运算求解能力.
点评：离心率是圆锥曲线中一个常考的内容，要重点把握.
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
设点
是以
为左、右焦点的双曲线
左支上一点，且满足
，则此双曲线的离心率为（ ）
A． | B． | C． | D． |
已知
, 
是椭圆
的两个焦点，点
在此椭圆上且
，则
的面积等于（ ）
A． | B． | C．2 | D． |
双曲线
－
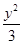＝1的渐近线与圆(x－3)2＋y2＝r2(r＞0)相切，则r＝（ ）
A． | B．2 | C．3 | D．6 |
椭圆
的焦点坐标是（ ）
A．(0, )、(0, ) | B． (0,-1)、(0,1) |
| C．(-1,0)、(1,0) | D．(,0)、(,0) |
已知抛物线的顶点在原点，焦点在y轴上，抛物线上的点
到焦点的距离等于5，
则m
A． | B． | C． | D． |
一动圆圆心在抛物线
上,且动圆恒与直线
相切,则动圆必过定点
A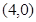． | B． | C． | D． |
下列曲线中，离心率为2的是（ ）
A． | B． | C． | D． |
过点(0，1)作直线，使它与抛物线y2=4x仅有一个公共点，这样的直线有( )
| A．1条 | B．2条 | C．3条 | D．4条 |