题目内容
设点 是以
是以 为左、右焦点的双曲线
为左、右焦点的双曲线 左支上一点,且满足
左支上一点,且满足 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )
A. | B. | C. | D. |
D
解析试题分析:设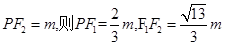 ,
,
考点:双曲线的简单性质;平面向量的数量积;双曲线离心率的求法。
点评:求圆锥曲线的离心率是常见题型,常用方法:①直接利用公式 ;②利用变形公式:
;②利用变形公式: (椭圆)和
(椭圆)和 (双曲线)③根据条件列出关于a、b、c的关系式,两边同除以a,利用方程的思想,解出
(双曲线)③根据条件列出关于a、b、c的关系式,两边同除以a,利用方程的思想,解出 。
。

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
双曲线 的渐近线方程为
的渐近线方程为
A.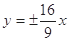 | B. | C. | D. |
中心在坐标原点的椭圆,焦点在x轴上,焦距为4,离心率为 ,则该椭圆的方程为
,则该椭圆的方程为
A. | B. | C. | D. |
已知双曲线 的两个焦点为
的两个焦点为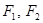 ,
, 为坐标原点,点
为坐标原点,点 在双曲线上,且
在双曲线上,且 ,若
,若 、
、 、
、 成等比数列,则
成等比数列,则 等于
等于
A. | B. | C. | D. |
顶点在原点,且过点 的抛物线的标准方程是
的抛物线的标准方程是
A. | B. |
C. 或 或 | D. 或 或 |
方程2x2+ky2=1表示的是焦点在y轴上的椭圆,则实数k的取值范围是( )
| A.(0,+∞) | B.(2,+∞) | C.(0,2) | D.(0,1) |
抛物线 的焦点坐标是( )
的焦点坐标是( )
A. | B. | C. | D. |
已知椭圆 (
( )中,
)中, 成等比数列,则椭圆的离心率为( )
成等比数列,则椭圆的离心率为( )
A. | B.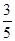 | C. | D. |
若椭圆的短轴为 ,一个焦点为
,一个焦点为 ,且
,且 为等边三角形的椭圆的离心率是( )
为等边三角形的椭圆的离心率是( )
A. | B. | C. | D.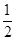 |