题目内容
16.给出下列3个命题:①若a,b∈R,则$\frac{a+b}{2}≥\sqrt{ab}$;②若x∈R,则x2+1>x;③若x∈R且x≠0,则x+$\frac{1}{x}$≥2,其中真命题的序号为②.分析 ①举例说明命题不成立;
②利用作差法证明命题正确;
③讨论x>0与x<0时,x+$\frac{1}{x}$的最值问题即可.
解答 解:对于①,当a<0,b<0时,$\frac{a+b}{2}≥\sqrt{ab}$不成立,∴①错误;
对于②,任意x∈R,有x2+1-x=${(x-\frac{1}{2})}^{2}$+$\frac{3}{4}$>0
∴x2+1>x,②正确;
对于③,当x>0时,x+$\frac{1}{x}$≥2,当x<0时,x+$\frac{1}{x}$≤-2;∴③错误
综上,真命题的序号是②.
故答案为:②.
点评 本题考查了不等式与不等关系的应用问题,也考查了分类讨论思想的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.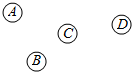 如图,A、B、C、D为四个村庄,要修筑三条公路,将这四个村庄连起来,则不同的修筑方法共有( )
如图,A、B、C、D为四个村庄,要修筑三条公路,将这四个村庄连起来,则不同的修筑方法共有( )
 如图,A、B、C、D为四个村庄,要修筑三条公路,将这四个村庄连起来,则不同的修筑方法共有( )
如图,A、B、C、D为四个村庄,要修筑三条公路,将这四个村庄连起来,则不同的修筑方法共有( )| A. | 8种 | B. | 12种 | C. | 16种 | D. | 20种 |
11.如图所示的是一串黑白相间排列的珠子,若按这种规律排列下去,那么第36颗珠子的颜色是 ( )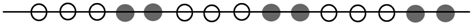
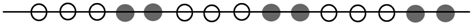
| A. | 白色 | B. | 黑色 | C. | 白色的可能性大 | D. | 黑色的可能性大 |
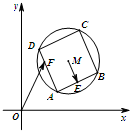 如图,已知圆M:(x-3)2+(y-3)2=4,四边形ABCD为圆M的内接正方形,E为边AB的中点,当正方形ABCD绕圆心M转动,同时点F在边AD上运动时,$\overrightarrow{ME}$$•\overrightarrow{OF}$的最大值是8.
如图,已知圆M:(x-3)2+(y-3)2=4,四边形ABCD为圆M的内接正方形,E为边AB的中点,当正方形ABCD绕圆心M转动,同时点F在边AD上运动时,$\overrightarrow{ME}$$•\overrightarrow{OF}$的最大值是8.