题目内容
【题目】对于定义域为D的函数![]() ,若同时满足下列条件:①
,若同时满足下列条件:①![]() 在D内单调递增或单调递减;②存在区间
在D内单调递增或单调递减;②存在区间![]() ,使
,使![]() 在
在![]() 上的值域为
上的值域为![]() .那么把
.那么把![]() 称为闭函数.下列结论正确的是( )
称为闭函数.下列结论正确的是( )
A.函数![]() 是闭函数
是闭函数
B.函数![]() 是闭函数
是闭函数
C.函数![]() 是闭函数
是闭函数
D.![]() 时,函数
时,函数![]() 是闭函数
是闭函数
E.![]() 时,函数
时,函数![]() 是闭函数
是闭函数
【答案】BD
【解析】
依次判断每个选项:根据单调性排除![]() ;
;![]() 在
在![]() 上的值域为
上的值域为![]() B正确;根据闭函数定义得到
B正确;根据闭函数定义得到![]() ,故D正确,E错误,得到答案.
,故D正确,E错误,得到答案.
因为![]() 在定义域
在定义域![]() 上不是单调函数,所以函数
上不是单调函数,所以函数![]() 不是闭函数,A错误;
不是闭函数,A错误;
![]() 在定义域上是减函数,由题意设
在定义域上是减函数,由题意设![]() ,则
,则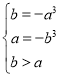 ,解得
,解得![]()
因此存在区间![]() ,使
,使![]() 在
在![]() 上的值域为
上的值域为![]() ,B正确;
,B正确;
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递增,所以函数在定义域上不单调递增或单调递减,从而该函数不是闭函数,C错误;
上单调递增,所以函数在定义域上不单调递增或单调递减,从而该函数不是闭函数,C错误;
若![]() 是闭函数,则存在区间
是闭函数,则存在区间![]() ,使函数
,使函数![]() 的值域为
的值域为![]() ,即
,即 ,所以a,b为方程
,所以a,b为方程![]() 的两个实数根,
的两个实数根,
即方程![]() 有两个不等的实根.
有两个不等的实根.
当![]() 时,有
时,有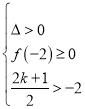 ,解得
,解得![]() ;
;
当![]() 时,有
时,有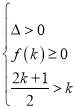 ,此不等式组无解.
,此不等式组无解.
综上所述,![]() ,因此D正确,E错误;
,因此D正确,E错误;
故选:BD

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案【题目】计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量X(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,如将年人流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(1)求未来4年中,至多有1年的年入流量超过120的概率;(![]() ,
,![]() )
)
(2)水电站希望安装的发电机尽可能运行最多,但每年发电机最多可运行台数受年入流量X限制,并有如下关系:
年流入量 |
|
|
|
发电机最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为4000万元,若某台发电机未运行,则该台年亏损600万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
【题目】总体由编号为01,02,03,![]() ,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的第4个个体的编号为( )
,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的第4个个体的编号为( )
78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
A. 05 B. 09 C. 07 D. 20
【题目】某公司最近4年对某种产品投入的宣传费![]() 万元与年销售量
万元与年销售量![]() 之间的关系如下表所示.
之间的关系如下表所示.
| 1 | 4 | 9 | 16 |
| 168.6 | 236.6 | 304.6 | 372.6 |
(1)根据以上表格中的数据判断:![]() 与
与![]() 哪一个更适宜作为
哪一个更适宜作为![]() 与
与![]() 的函数模型?
的函数模型?
(2)已知这种产品的年利润![]() 万元与
万元与![]() 的关系为
的关系为![]() ,则年宣传费
,则年宣传费![]() 为多少时年利润最大?
为多少时年利润最大?
【题目】手机厂商推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下:
女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 20 | 40 | 80 | 50 | 10 | |
男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
频数 | 45 | 75 | 90 | 60 | 30 |
(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的波动大小(不计算具体值,给出结论即可);

(2)把评分不低于70分的用户称为“评分良好用户”,能否有![]() 的把握认为“评分良好用户”与性别有关?
的把握认为“评分良好用户”与性别有关?
参考附表:
|
|
|
|
|
|
|
|
|
|
参考公式 ,其中
,其中![]()

