题目内容
已知圆C过点P(1，1)，且与圆M：(x＋2)2＋(y＋2)2＝r2(r＞0)关于直线x＋y＋2＝0对称．
(1)求圆C的方程；
(2)过点P作两条相异直线分别与圆C相交于A、B，且直线PA和直线PB的倾斜角互补，O为坐标原点，试判断直线OP和AB是否平行？请说明理由．
(1)求圆C的方程；
(2)过点P作两条相异直线分别与圆C相交于A、B，且直线PA和直线PB的倾斜角互补，O为坐标原点，试判断直线OP和AB是否平行？请说明理由．
（1）x2＋y2＝2（2）一定平行
(1)设圆心C(a，b)，则
解得
则圆C的方程为x2＋y2＝r2，
将点P的坐标代入得r2＝2，故圆C的方程为x2＋y2＝2.，
(2)由题意知，直线PA和直线PB的斜率存在，且互为相反数，故可设PA：y－1＝k(x－1)，
PB：y－1＝－k(x－1)，由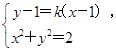
得(1＋k2)x2＋2k(1－k)x＋(1－k)2－2＝0.因为点P的横坐标x＝1一定是该方程的解，故可得xA＝
.同理可得xB＝
，所以kAB＝
＝1＝kOP，
所以，直线AB和OP一定平行．
解得则圆C的方程为x2＋y2＝r2，将点P的坐标代入得r2＝2，故圆C的方程为x2＋y2＝2.，
(2)由题意知，直线PA和直线PB的斜率存在，且互为相反数，故可设PA：y－1＝k(x－1)，
PB：y－1＝－k(x－1)，由
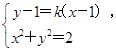得(1＋k2)x2＋2k(1－k)x＋(1－k)2－2＝0.因为点P的横坐标x＝1一定是该方程的解，故可得xA＝.同理可得xB＝，所以kAB＝＝1＝kOP，所以，直线AB和OP一定平行．
练习册系列答案
黄冈小状元解决问题天天练系列答案
相关题目
的圆心在直线
上，且与
轴交于两点
,
.
的圆
，点
在圆
,
为一组邻边的平行四边形的另一个顶点
轨迹方程.
上，圆C过坐标原点O，且与x轴、y轴交于A、B两点，则△OAB的面积是( )
△
中，
以
为直径的圆交
于
，则
的长为（ ）
