题目内容
夹在两条平行线l1:3x-4y=0与l2:3x-4y-20=0之间的圆的最大面积为 .
4π
由题意,得l1:3x-4y=0与l2:3x-4y-20=0之间的距离为:d=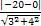
=4.
当两条平行线间的圆与两直线都相切时,圆面积最大,
∴圆的最大直径为2R=4⇒最大半径R=2,
可得最大圆的面积为S=πR2=4π.
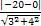=4.当两条平行线间的圆与两直线都相切时,圆面积最大,
∴圆的最大直径为2R=4⇒最大半径R=2,
可得最大圆的面积为S=πR2=4π.
练习册系列答案
相关题目
(a>0,b>0)与y轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为________.
x2-
x+1与x轴正半轴的交点分别为A,B,与y轴正半轴的交点是C,则过A,B,C三点的圆的标准方程是 .
的半径为( )
的圆
中，弦
、
相交于
，
，
，则圆心