题目内容
已知圆C的圆心在曲线y= 上,圆C过坐标原点O,且与x轴、y轴交于A、B两点,则△OAB的面积是( )
上,圆C过坐标原点O,且与x轴、y轴交于A、B两点,则△OAB的面积是( )
A.2 B.3 C.4 D.8
 上,圆C过坐标原点O,且与x轴、y轴交于A、B两点,则△OAB的面积是( )
上,圆C过坐标原点O,且与x轴、y轴交于A、B两点,则△OAB的面积是( )A.2 B.3 C.4 D.8
C
设圆心C的坐标是(t, ).
).
∵圆C过坐标原点,∴|OC|2=t2+ ,
,
设圆C的方程是
(x-t)2+(y- )2=t2+
)2=t2+ .
.
令x=0,得y1=0,y2= ,
,
故B点的坐标为(0, ).
).
令y=0,得x1=0,x2=2t,
故A点的坐标为(2t,0),
∴S△OAB= |OA|·|OB|=
|OA|·|OB|= ×|
×| |×|2t|=4,即△OAB的面积为4.故选C.
|×|2t|=4,即△OAB的面积为4.故选C.
 ).
).∵圆C过坐标原点,∴|OC|2=t2+
 ,
,设圆C的方程是
(x-t)2+(y-
 )2=t2+
)2=t2+ .
.令x=0,得y1=0,y2=
 ,
,故B点的坐标为(0,
 ).
).令y=0,得x1=0,x2=2t,
故A点的坐标为(2t,0),
∴S△OAB=
 |OA|·|OB|=
|OA|·|OB|= ×|
×| |×|2t|=4,即△OAB的面积为4.故选C.
|×|2t|=4,即△OAB的面积为4.故选C.
练习册系列答案
相关题目
 的直径
的直径 的长为4,点
的长为4,点 平分弧
平分弧 ,过
,过 ,交
,交 .
. :
: 的角平分线,求
的角平分线,求 的长.
的长.
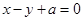 与圆心为
与圆心为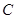 的圆
的圆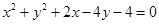 相交于
相交于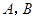 两点,且
两点,且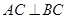 ,则实数
,则实数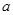 的值为_________.
的值为_________. (a>0,b>0)与y轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为________.
(a>0,b>0)与y轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为________.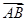 =3
=3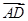 ,E、F为另一直径的两个端点,则
,E、F为另一直径的两个端点,则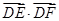 =( )
=( )