题目内容
（本小题共12分）
已知△ABC顶点的直角坐标分别为A（3，4），B（0，0），C（c，0）
（1）若c=5，求sin∠A的值；
（2）若∠A是钝角，求c的取值范围。
（1）
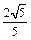
（2）
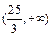
解析
练习册系列答案
名校课堂系列答案
相关题目
名校课堂系列答案题目内容
（本小题共12分）
已知△ABC顶点的直角坐标分别为A（3，4），B（0，0），C（c，0）
（1）若c=5，求sin∠A的值；
（2）若∠A是钝角，求c的取值范围。
（1）
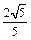
（2）
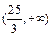
解析
名校课堂系列答案
中，角A、B、C所对的边分别为
、
、
，
的值； （2）求
中，内角
对边的边长分别是
，且
,
（2）若边
且
，求
的值．(12分)
处测得某岛
的方位角为北偏东
角，前进
后在
处测得该岛的方位角为北偏东
角，已知该岛周围
，问该船有无触礁危险？如果没有，请说明理由；如果有，那么该船自
中内角
、
、
的对边分别为
、
、
，向量m
，n
且m
n
，求
的最大值。
的内角
的对边分别为
，且
，
,求：
的值；
的值．
且
，三角形面积
，求
的值。