题目内容
2．某同学想要作一个三边上的高分别为15、21、35的三角形，则下列说法正确的是（ ）| A． | 可以做出这样的三角形，且最大内角为$\frac{5π}{6}$ | |
| B． | 可以做出这样的三角形，且最大内角为$\frac{3π}{4}$ | |
| C． | 可以做出这样的三角形，且最大内角为$\frac{2π}{3}$ | |
| D． | 不可能做出这样的三角形 |
分析 假设存在这样的三角形，三条边分别为a、b、c，由三角形的面积公式可得a=$\frac{7}{3}$c，b=$\frac{5}{3}$c，由三角形的三边关系和余弦定理可得．
解答 解：假设存在这样的三角形，三条边分别为a、b、c，
则由三角形的面积公式可得S=$\frac{1}{2}$×a×15=$\frac{1}{2}$×b×21=$\frac{1}{2}$×c×35，
解得a=$\frac{7}{3}$c，b=$\frac{5}{3}$c，可得b+c=$\frac{8}{3}$c＞a，故存在这样的三角形，
由余弦定理可得最大角A的余弦值cosA=$\frac{（\frac{5c}{3}）^{2}+{c}^{2}-（\frac{7c}{3}）^{2}}{2×\frac{5c}{3}×c}$=-$\frac{1}{2}$，
∴最大内角A=$\frac{2π}{3}$
故选：C．
点评 本题考查解三角形，涉及三边关系和余弦定理以及三角形的面积公式，属基础题．
练习册系列答案
相关题目
12．在如图所示的程序框图中，若输出的S=9，则n=（ ）
| A． | 101 | B． | 100 | C． | 99 | D． | 98 |
13．cos80°cos130°-sin80°sin130°等于（ ）
| A． | -$\frac{{\sqrt{3}}}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
10．点A（1，2，3）关于xOy平面对称的点B坐标是（ ）
| A． | （-1，2，3） | B． | （1，-2，3） | C． | （1，2，-3） | D． | （-1，-2，3） |
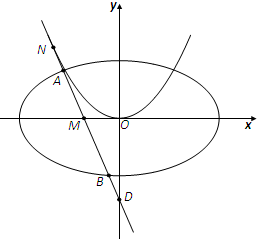椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，且以原点为圆心，椭圆的短半轴长为半径的圆与直线x-y+$\sqrt{2}$=0相切．