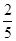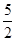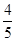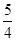题目内容
顶点在原点,经过圆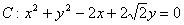 的圆心且准线与
的圆心且准线与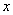 轴垂直的抛物线方程为
轴垂直的抛物线方程为
A.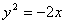 | B.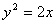 |
C.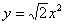 | D.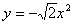 |
B
解析试题分析:圆的方程化为标准方程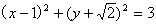 ,圆心为
,圆心为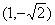 ,设抛物线方程为
,设抛物线方程为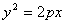 ,即
,即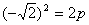 ,故
,故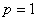 ,所以抛物线方程为
,所以抛物线方程为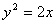 .
.
考点:抛物线的简单性质;抛物线的标准方程.
点评:本题是基础题,考查抛物线的标准方程的求法,注意标准方程的形式,是易错题,考查计算能力.

练习册系列答案
相关题目
知圆柱的底面半径为2,高为3,用一个平面去截,若所截得的截面为椭圆,则椭圆的离心率的取值范围为( )
A. | B.(0, | C. | D.(0,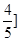 |
双曲线 的渐近线方程为( )
的渐近线方程为( )
A. | B. | C. | D. |
已知抛物线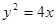 和点
和点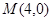 ,
, 为抛物线上的点,则满足
为抛物线上的点,则满足 的点
的点 有( )个。
有( )个。
A. | B.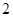 | C.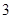 | D. |
抛物线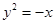 的焦点坐标为( )
的焦点坐标为( )
A.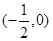 | B.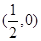 | C.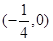 | D.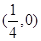 |
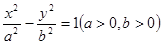 的左右焦点分别是
的左右焦点分别是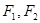 ,设
,设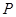 是双曲线右支上一点,
是双曲线右支上一点,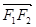 在
在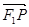 上投影的大小恰好为
上投影的大小恰好为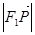 ,且它们的夹角为
,且它们的夹角为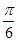 ,则双曲线的离心率为( )
,则双曲线的离心率为( )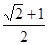
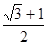
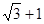
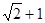
 (
(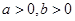 )的右焦点
)的右焦点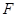 作圆
作圆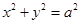 的切线
的切线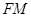 ,交
,交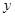 轴于点
轴于点 ,切圆于点
,切圆于点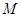 ,若
,若 ,则双曲线的离心率是( )
,则双曲线的离心率是( )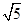


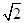
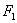 、
、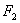 是一对相关曲线的焦点,
是一对相关曲线的焦点,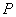 是它们在第一象限的交点,当
是它们在第一象限的交点,当 时,这一对相关曲线中双曲线的离心率是( )
时,这一对相关曲线中双曲线的离心率是( )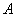 .
.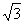
 .
.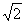
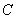 .
.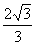
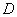 .
.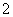
 为双曲线
为双曲线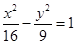 的左焦点,在
的左焦点,在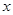 轴上
轴上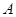 ,以
,以 为直径的圆与双曲线左、右两支在
为直径的圆与双曲线左、右两支在 、
、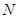 ,则
,则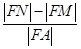 的值为( )
的值为( )