题目内容
【题目】已知圆C经过P(4,-2),Q(-1,3)两点,且圆心C在直线x+y-1=0上.
(1)求圆C的方程;
(2)若直线l∥PQ,且l与圆C交于点A,B且以线段AB为直径的圆经过坐标原点,求直线l的方程.
【答案】(1)![]() (2)y=-x+4或y=-x-3
(2)y=-x+4或y=-x-3
【解析】
(1)由圆的性质知圆心在线段![]() 的垂直平分线上,因此可求得线段
的垂直平分线上,因此可求得线段![]() 的垂直平分线的方程,与方程
的垂直平分线的方程,与方程![]() 联立,可求得圆心坐标,再求得半径后可得圆标准方程;
联立,可求得圆心坐标,再求得半径后可得圆标准方程;
(2)设![]() 的方程为
的方程为![]() .代入圆方程,设A(x1,y1),B(x2,y2),则x1+x2=m+1,x1x2=
.代入圆方程,设A(x1,y1),B(x2,y2),则x1+x2=m+1,x1x2=![]() -6.而以线段AB为直径的圆经过坐标原点,则有
-6.而以线段AB为直径的圆经过坐标原点,则有![]() ,即
,即![]() ,由此可求得
,由此可求得![]() ,得直线方程.
,得直线方程.
(1)∵P(4,-2),Q(-1,3),
∴线段PQ的中点M![]() ,斜率kPQ=-1,
,斜率kPQ=-1,
则PQ的垂直平分线方程为![]() ,
,
即![]() .
.
解方程组![]()
得![]()
∴圆心C(1,0),半径![]() .
.
故圆C的方程为![]() .
.
(2)由l∥PQ,设l的方程为![]() .
.
代入圆C的方程,得![]() .
.
设A(x1,y1),B(x2,y2),
则x1+x2=m+1,x1x2=![]() -6.
-6.
故y1y2=(m-x1)(m-x2)=m2+x1x2-m(x1+x2),
依题意知OA⊥OB,则![]() .
.
∴(x1,y1)·(x2,y2)=x1x2+y1y2=0,
于是m2+2x1x2-m(x1+x2)=0,即m2-m-12=0.
∴m=4或m=-3,经检验,满足Δ>0.
故直线l的方程为y=-x+4或y=-x-3.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案【题目】现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,
9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
7527 | 0293 | 7140 | 9857 | 0347 | 4373 | 8636 | 6947 | 1417 | 4698 |
0371 | 6233 | 2616 | 8045 | 6011 | 3661 | 9597 | 7424 | 7610 | 4281 |
根据以上数据估计该射击运动员射击4次至少击中3次的概率为_______.
【题目】某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见下表.
内,发布成绩使用等级制,各等级划分标准见下表.
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | A | B | C | D |
规定:A,B,C三级为合格等级,D为不合格等级为了解该校高三年级学生身体素质情况,从中抽取了n名学生的原始成绩作为样本进行统计.
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
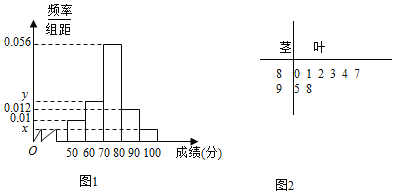
![]() 求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
![]() 根据频率分布直方图,求成绩的中位数
根据频率分布直方图,求成绩的中位数![]() 精确到
精确到![]() ;
;
![]() 在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.