题目内容
20．若复数1-$\sqrt{3}i$（i为虚数单位），是z的共轭复数，则在复平面内，复数z对应的点的坐标为（ ）| A． | （0，1） | B． | （1，-$\sqrt{3}$） | C． | （-1，-$\sqrt{3}$） | D． | （-1，0） |
分析 直接求出复数的共轭复数，然后推出对应点的坐标即可．
解答 解：复数1-$\sqrt{3}i$（i为虚数单位），是z的共轭复数，
可得z=-1-$\sqrt{3}$i．
在复平面内，复数z对应的点的坐标为：（-1，-$\sqrt{3}$）．
故选：C．
点评 本题考查复数的几何意义，复数的概念，考查基本知识的应用．
练习册系列答案
小夫子全能检测系列答案
相关题目
11．
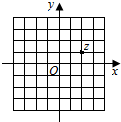若i为虚数单位，图中网格纸的小正方形的边长是1，复平面内点Z表示复数z，那么复数$\frac{z}{1+i}$对应的点位于复平面内的（ ）
若i为虚数单位，图中网格纸的小正方形的边长是1，复平面内点Z表示复数z，那么复数$\frac{z}{1+i}$对应的点位于复平面内的（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
5．已知函数f（x）=$\left\{\begin{array}{l}\frac{2}{x}，x≥2\\{（x-1）^3}，0＜x＜2\end{array}\right.$，若关于x的方程f（x）=kx有两个不同的实根，则实数k的取值范围是（ ）
| A． | $（{0，\frac{1}{2}}）$ | B． | $（{0，\frac{{\sqrt{2}}}{4}}）∪（{\frac{{\sqrt{2}}}{4}，\frac{1}{2}}）$ | C． | $（{\frac{{\sqrt{2}}}{4}，+∞}）$ | D． | $[{\frac{1}{2}，2\sqrt{2}}]$ |
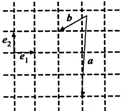已知向量$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$、$\overrightarrow{a}$、$\overrightarrow{b}$如图所示，以$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为基底，则$\overrightarrow{a}$-$\overrightarrow{b}$可表示为$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$．