题目内容
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
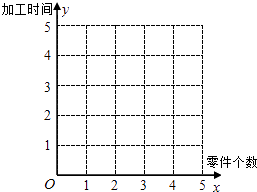
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间? 参考公式:回归直线 ![]() =bx+a,其中b=
=bx+a,其中b= 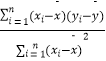 =
= 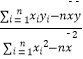 ,a=
,a= ![]() ﹣b
﹣b ![]() .
.
【答案】
(1)解:作出散点图如下:
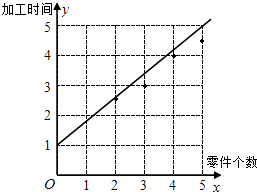
(2)解: ![]() =
= ![]() (2+3+4+5)=3.5,
(2+3+4+5)=3.5, ![]() =
= ![]() (2.5+3+4+4.5)=3.5,
(2.5+3+4+4.5)=3.5,
![]() =54,
=54, ![]() xiyi=52.5
xiyi=52.5
∴b= ![]() =0.7,a=3.5﹣0.7×3.5=1.05,
=0.7,a=3.5﹣0.7×3.5=1.05,
∴所求线性回归方程为:y=0.7x+1.05
(3)解:当x=10代入回归直线方程,得y=0.7×10+1.05=8.05(小时).
∴加工10个零件大约需要8.05个小时
【解析】(1)根据表中所给的数据,可得散点图;(2)求出出横标和纵标的平均数,得到样本中心点,求出对应的横标和纵标的积的和,求出横标的平方和,做出系数和a的值,写出线性回归方程.(3)将x=10代入回归直线方程,可得结论.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目